题目内容
10. 在一次水稻试验田验收活动中,将甲、乙两种水稻随机抽取各6株样品,单株籽粒数制成如图所示的茎叶图:
在一次水稻试验田验收活动中,将甲、乙两种水稻随机抽取各6株样品,单株籽粒数制成如图所示的茎叶图:(Ⅰ)一粒水稻约为0.1克,每亩水稻约为6万株,估计甲种水稻亩产约为多少公斤?
(Ⅱ)分别从甲、乙两种水稻样品中任取一株,甲品种中选出的籽粒数记为a,乙品种中选出的籽粒数记为b,求a≥b的概率.
(Ⅲ)如从甲品种的6株中任选2株,记选到的超过187粒的株数为ξ,求ξ的分布列和数学期望.
分析 (Ⅰ)由茎叶图能估计甲种水稻亩产.
(Ⅱ)分别从甲、乙两种水稻样品中任取一株,先求出基本事件总数,再求出a≥b包含的基本事件个数,由此能求出a≥b的概率.
(Ⅲ)由已知得ξ的可能取值为0,1,2.分别求出相应的概率,由此能求出ξ的分布列和Eξ.
解答 解:(Ⅰ)由茎叶图估计甲种水稻亩产约为:
[$\frac{1}{6}$(168+176+179+186+188+195)×0.1×60000]×$\frac{1}{1000}$=1092(公斤).
(Ⅱ)分别从甲、乙两种水稻样品中任取一株,基本事件总数n=6×6=36,
甲品种中选出的籽粒数记为a,乙品种中选出的籽粒数记为b,
a≥b包含的基本事件个数m=2+2+5+5+6=20,
∴a≥b的概率p=$\frac{20}{36}=\frac{5}{9}$.
(Ⅲ)由已知得ξ的可能取值为0,1,2.
P(ξ=0)=$\frac{{C}_{4}^{2}}{{C}_{6}^{2}}$=$\frac{6}{15}$,
P(ξ=1)=$\frac{{C}_{4}^{1}{C}_{2}^{1}}{{C}_{6}^{2}}$=$\frac{8}{15}$,
P(ξ=2)=$\frac{{C}_{2}^{2}}{{C}_{6}^{2}}$=$\frac{1}{15}$,
∴ξ的分布列为:
| ξ | 0 | 1 | 2 |
| P | $\frac{6}{15}$ | $\frac{8}{15}$ | $\frac{1}{15}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.

练习册系列答案
相关题目
20.在△ABC中,AB=2,AC=1,∠A=$\frac{2π}{3}$,过A作AD⊥BC于D,且$\overrightarrow{AD}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则λμ=( )
| A. | $\frac{10}{49}$ | B. | $\frac{5\sqrt{7}}{14}$ | C. | $\frac{9}{7}$ | D. | 1 |
18.在等比数列{an}中,已知a4=27a3,则$\frac{{a}_{2}}{{a}_{1}}$+$\frac{{a}_{4}}{{a}_{2}}$+$\frac{{a}_{6}}{{a}_{3}}$+…+$\frac{{a}_{2n}}{{a}_{n}}$等于( )
| A. | $\frac{{3}^{-n}-3}{2}$ | B. | $\frac{{3}^{1-n}-3}{2}$ | C. | $\frac{{3}^{n}-3}{2}$ | D. | $\frac{{3}^{n+1}-3}{2}$ |
15.已知向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(2,-3).若向量$\overrightarrow{c}$满足$\overrightarrow{c}$⊥($\overrightarrow{a}$+$\overrightarrow{b}$),且$\overrightarrow{b}$∥($\overrightarrow{a}$-$\overrightarrow{c}$),则$\overrightarrow{c}$=( )
| A. | $(\frac{7}{9},\frac{7}{3})$ | B. | $(-\frac{7}{9},\frac{7}{3})$ | C. | $(\frac{7}{9},-\frac{7}{3})$ | D. | $(-\frac{7}{9},-\frac{7}{3})$ |
19.已知函数f(x)定义域为R,则命题p:“函数f(x)为偶函数”是命题q:“?x0∈R,f(x0)=f(-x0)”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
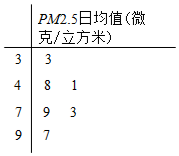 PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国PM2.5标准采用世卫组织设定的最宽限值,PM2.5日均值在35微克/立方米以下空气质量为1级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米及其以上空气质量为超标.
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国PM2.5标准采用世卫组织设定的最宽限值,PM2.5日均值在35微克/立方米以下空气质量为1级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米及其以上空气质量为超标.