题目内容
已知不等式x+3≥0的解集是A，则使得a∈A是假命题的a的取值范围是（ ）
| A、a≥-3 | B、a＞-3 |
| C、a≤-3 | D、a＜-3 |
考点：命题的真假判断与应用,元素与集合关系的判断
专题：简易逻辑
分析：利用不等式的解法和命题的否定即可得出．
解答：
解：不等式x+3≥0的解集是{x|x≥-3}，
即A={x|x≥-3}．
因此使得a∈A是假命题的a的取值范围是a＜-3．
故选：D．
即A={x|x≥-3}．
因此使得a∈A是假命题的a的取值范围是a＜-3．
故选：D．
点评：本题考查了不等式的解法和命题的否定，属于基础题．
练习册系列答案
金博士一点全通系列答案
相关题目
如图在四面体ABCD中，若截面PQMN是正方形，则在下列命题中正确的有已知O为坐标原点，P1、P2是双曲线
-
=1上的点．P是线段P1P2的中点，直线OP、P1P2的斜率分别为k1、k2，若2≤k1≤4，则k2的取值范围是（ ）
| x2 |
| 9 |
| y2 |
| 4 |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
“非空集合M的元素都是集合P的元素”是假命题，则以下四个命题：
（1）M的元素都不是P的元素；
（2）M中有不属于P元素；
（3）M中有P的元素；
（4）M的元素不都是P的元素，
其中真命题的个数有（ ）
（1）M的元素都不是P的元素；
（2）M中有不属于P元素；
（3）M中有P的元素；
（4）M的元素不都是P的元素，
其中真命题的个数有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
集合A={x|1＜x＜3}，B={x|x≤2}，则A∩B=（ ）
| A、{x|x＜3} |
| B、{x|2≤x＜3} |
| C、{x|1＜x≤2} |
| D、{x|1＜x＜2} |
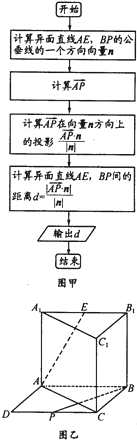在直三棱柱（侧面垂直于底面的三棱柱）ABC-A1B1C1中，以AB、BC为邻边作平行四边形ABCD，AB⊥BC，AB=BC=AA1记线段CD、A1B1的中心分别是P、E连接AE、BP，得到如图所示的几何体