题目内容
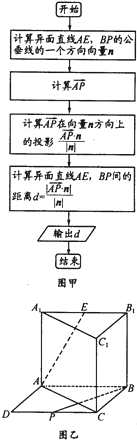 在直三棱柱(侧面垂直于底面的三棱柱)ABC-A1B1C1中,以AB、BC为邻边作平行四边形ABCD,AB⊥BC,AB=BC=AA1记线段CD、A1B1的中心分别是P、E连接AE、BP,得到如图所示的几何体
在直三棱柱(侧面垂直于底面的三棱柱)ABC-A1B1C1中,以AB、BC为邻边作平行四边形ABCD,AB⊥BC,AB=BC=AA1记线段CD、A1B1的中心分别是P、E连接AE、BP,得到如图所示的几何体(1)若AA1=a,图甲给出了异面直线之间的距离的一种算法框图(其中异面直线的公垂线是指两异面直线都垂直且相交的直线)请利用这种方法求异面直线AE和BP之间的距离;
(2)若AA1=2,在线段A1P上是否存在一点F,使得平面AFB⊥平面A1BP?若存在,指出点F的位置,并证明你的结论;若不存在,请说明理由;
(3)若AA1=a,在线段A1C上有一M,过点M做垂直于平面A1ACC1的直线l,与直三棱柱ABC-A1B1C1的其他侧面相交于N,过CM=x,MN=y,求函数y=f(x)的解析式,并据此求出线段MN的长度最大值.
考点:点、线、面间的距离计算
专题:空间向量及应用
分析:(1)分别以AD、AB、AA1为x,y,z轴,建立空间直角坐标系,利用向量法能求出异面直线AE和BP之间的距离.
(2)假设在线段A1P上存在满足题意的点F,设F(x,y,z),分别求出平面A1BP的一个法向量和平面AEB的一个法向量,再利用向量法进行计算.
(3)根据题意作出图,分0≤x≤
a和
a<x≤
a两种情况进行分类讨论,由此能求出函数y=f(x)的解析式,并据此求出线段MN的长度最大值.
(2)假设在线段A1P上存在满足题意的点F,设F(x,y,z),分别求出平面A1BP的一个法向量和平面AEB的一个法向量,再利用向量法进行计算.
(3)根据题意作出图,分0≤x≤
| ||
| 2 |
| ||
| 2 |
| 3 |
解答:
解:(1)由题意知四边形ABCD为正方形,
∴AD,AB,AA1三线两两垂直,
分别以AD、AB、AA1为x,y,z轴,建立空间直角坐标系,
则由题意知A(0,0,0),E(0,
,a),B(0,a,0),P(a,
,0),
设异面直线AE与BP的一个法向量为
=(x,y,z),
则
•
=0,
•
=0,
∴
,∴
=(1,2,-1),
又∵
=(a,
,0),
∴异面直线AE和BP之间的距离:
d=
=
=
a.
(2)∵AA1=2,∴A1(0,0,2),P(2,1,0),B(0,2,0),
∴
=(2,1,-2),
=(0,2,-2),
设平面A1BP的一个法向量为
=(x1,y1,z1),
则
,
∴
=(1,2,2),
假设在线段A1P上存在满足题意的点F,设F(x,y,z),
由
=λ
,(0≤λ≤1),
即(x,y,z-2)=λ(2,1,-2),
得x=2λ,y=λ,z=2-2λ,
∴F(2λ,λ,2-2λ),
则
=(2λ,λ,2-2λ),
=(0,2,0),
设平面AEB的一个法向量
=(x2,y2,z2),
则
,
∴
=(λ-1,0,λ),
∵平面AFB⊥平面A1BP,
∴
•
=λ-1+2λ=0,解得λ=
.
∴存在这样的点,
当点F为线段A1P上靠近A1的一个三等分点时,符合题意.
(3)根据题意作出图如图1,
①当0≤x≤
a时,
把MN向平面ABC内正投影得到M′N′,如图2,
则MN=M′N′,
∵
=
=
=
,
∴CM′=
x
在等腰直角三角形M′N′C中,M‘N’=CM‘=
x,
∴MN=
x,
∴当0≤x≤
a时,y=
x.
②当
a<x≤
a时,
把MN向平面ABC内正投影得到M′N′,如图3,
则MN=M′N′,
∵
=
=
=
,
∴AM′=
(
a-x),
在等股直角三角形M′N′A中,
M′N′=AM′=
(
a-x),
∴MN=
(
a-x),
∴当
a<x≤
a时,MN=
(
a-x).
综上所述,y=
,
∴当x=
a时,ymax=
a.

∴AD,AB,AA1三线两两垂直,
分别以AD、AB、AA1为x,y,z轴,建立空间直角坐标系,
则由题意知A(0,0,0),E(0,
| a |
| 2 |
| a |
| 2 |
设异面直线AE与BP的一个法向量为
| n |
则
| AE |
| n |
| BP |
| n |
∴
|
| n |
又∵
| AP |
| a |
| 2 |
∴异面直线AE和BP之间的距离:
d=
|
| ||||
|
|
| |a+a+0| | ||
|
| ||
| 3 |
(2)∵AA1=2,∴A1(0,0,2),P(2,1,0),B(0,2,0),
∴
| A1P |
| A1B |
设平面A1BP的一个法向量为
| n1 |
则
|
∴
| n1 |
假设在线段A1P上存在满足题意的点F,设F(x,y,z),
由
| A1F |
| A1P |
即(x,y,z-2)=λ(2,1,-2),
得x=2λ,y=λ,z=2-2λ,
∴F(2λ,λ,2-2λ),
则
| AF |
| AB |
设平面AEB的一个法向量
| n2 |
则
|
∴
| n2 |
∵平面AFB⊥平面A1BP,

∴
| n1 |
| n2 |
| 1 |
| 3 |
∴存在这样的点,
当点F为线段A1P上靠近A1的一个三等分点时,符合题意.
(3)根据题意作出图如图1,
①当0≤x≤
| ||
| 2 |
把MN向平面ABC内正投影得到M′N′,如图2,
则MN=M′N′,
∵
| CM′ |
| CM |
| CA |
| CA1 |
| ||
|
| ||
| 3 |
∴CM′=
| ||
| 3 |

在等腰直角三角形M′N′C中,M‘N’=CM‘=
| ||
| 3 |
∴MN=
| ||
| 3 |
∴当0≤x≤
| ||
| 2 |
| ||
| 3 |
②当
| ||
| 2 |
| 3 |
把MN向平面ABC内正投影得到M′N′,如图3,
则MN=M′N′,
∵
| AM′ |
| A1M |
| CA |
| CA1 |
| ||
|
| ||
| 3 |
∴AM′=
| ||
| 3 |
| 3 |
在等股直角三角形M′N′A中,
M′N′=AM′=
| ||
| 3 |
| 3 |
∴MN=
| ||
| 3 |
| 3 |
∴当
| ||
| 2 |
| 3 |
| ||
| 3 |
| 3 |
综上所述,y=
|
∴当x=
| ||
| 2 |
| ||
| 2 |
点评:本题考查异面直线的距离的求法,考查满足条件的点的确定,考查函数解析式的求法,解题时要注意空间思维能力的培养.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
已知不等式x+3≥0的解集是A,则使得a∈A是假命题的a的取值范围是( )
| A、a≥-3 | B、a>-3 |
| C、a≤-3 | D、a<-3 |
执行如图的程序框图,若输入的x值为7,则输出的x的值为( )


| A、2 | ||
| B、3 | ||
| C、log23 | ||
D、
|