题目内容
已知函数f(x)=sin2x+
cosxsinx-
,x∈R
(1)求函数f(x)的最小正周期
(2)在△ABC中,角A,B,C的对边分别为a,b,c,且满足2bcosA=2c-
a,求f(B)的值.
| 3 |
| 1 |
| 2 |
(1)求函数f(x)的最小正周期
(2)在△ABC中,角A,B,C的对边分别为a,b,c,且满足2bcosA=2c-
| 3 |
考点:余弦定理,三角函数中的恒等变换应用,三角函数的周期性及其求法
专题:三角函数的求值
分析:(1)函数解析式利用二倍角的正弦、余弦函数公式化简,整理为一个角的正弦函数,找出ω的值,代入周期公式即可求出最小正周期;
(2)已知等式利用正弦定理化简,整理后根据sinA不为0求出cosB的值,确定出B度数,即可求出f(B)的值.
(2)已知等式利用正弦定理化简,整理后根据sinA不为0求出cosB的值,确定出B度数,即可求出f(B)的值.
解答:
解:(1)f(x)=
+
sin2x-
=
sin2x-
cos2x
=sin(2x-
),
∵ω=2,
∴T=
=π;
(2)已知等式利用正弦定理化简得:2sinBcosA=2sinC-
sinA,
即2sinBcosA=2sin(A+B)-
sinA=2sinAcosB+2cosAsinB-
sinA,
整理得:2sinAcosB=
sinA,
∵sinA≠0,
∴cosB=
,
∴B=
,
则f(B)=sin(2B-
)=sin
=
.
| 1-cos2x |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
=
| ||
| 2 |
| 1 |
| 2 |
=sin(2x-
| π |
| 6 |
∵ω=2,
∴T=
| 2π |
| 2 |
(2)已知等式利用正弦定理化简得:2sinBcosA=2sinC-
| 3 |
即2sinBcosA=2sin(A+B)-
| 3 |
| 3 |
整理得:2sinAcosB=
| 3 |
∵sinA≠0,
∴cosB=
| ||
| 2 |
∴B=
| π |
| 6 |
则f(B)=sin(2B-
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
点评:此题考查了正弦定理,三角函数的周期性及其求法,两角和与差的正弦函数公式,以及特殊角的三角函数值,熟练掌握正弦定理是解本题的关键.

练习册系列答案
相关题目
已知函数f(x)=(
)x-
,正实数a、b、c满足f(c)<0<f(a)<f(b),若实数d是函数f(x)的一个零点,那么下列5个判断:①d<a;②d>b;③d<c;④c<a;⑤a>b.其中可能成立的个数为( )
| 1 |
| 4 |
| x |
| A、4 | B、3 | C、2 | D、1 |
已知不等式x+3≥0的解集是A,则使得a∈A是假命题的a的取值范围是( )
| A、a≥-3 | B、a>-3 |
| C、a≤-3 | D、a<-3 |
在△ABC中,如果a,b,c分别是角A,B,C的对边,设命题p:(a2+b2)sin(A-B)=(a2-b2)sin(A+B);命题q:△ABC为直角三角形,那么命题p是命题q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
复数(i-1)2等于( )
| A、-2i | B、2i |
| C、2-2i | D、2+2i |
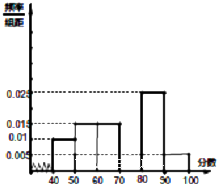 某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),[90,100]后画出如下部分频率颁布直方图,观察图形的信息,回答下列问题:
某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),[90,100]后画出如下部分频率颁布直方图,观察图形的信息,回答下列问题: