题目内容
 如图,四棱锥A-BCDE,平面ABC⊥平面BCDE,△ABC边长为2的等边三角形,底面BCDE是矩形,且CD=
如图,四棱锥A-BCDE,平面ABC⊥平面BCDE,△ABC边长为2的等边三角形,底面BCDE是矩形,且CD=| 2 |
(Ⅰ)若点G是AE的中点,求证:AC∥平面BDG;
(Ⅱ)试问点F在线段AB上什么位置时,二面角B-CE-F的大小为
| π |
| 4 |
考点:二面角的平面角及求法,直线与平面平行的判定
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)利用三角形的中位线定理和线面平行的判定定理即可证明;
(Ⅱ)建立空间直角坐标系,求平面BCE和CEF的法向量,利用向量法求二面角的大小,解方程即可得出.
(Ⅱ)建立空间直角坐标系,求平面BCE和CEF的法向量,利用向量法求二面角的大小,解方程即可得出.
解答:
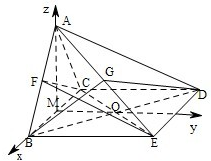 (Ⅰ)证明:连CE交BD于点M,∵四边形BCDE是矩形,M为CE中点,
(Ⅰ)证明:连CE交BD于点M,∵四边形BCDE是矩形,M为CE中点,
在△ACE中,G为AE中点,故GM∥AC.
∵GM?平面BDG,AC?平面BDG,∴AC∥平面BDG.
(Ⅱ)解:取BC中点O,分别以OB,OM,OA所在的直线为x,y,z轴建立空间直角坐标系,则A(0,0,
),B(1,0,0),C(-1,0,0),E(1,
,0)设
=λ
(0≤λ≤1),得F(1-λ,0,
λ),显然平面BCE的法向量为(0,0,1)
设平面CEF的法向量为
=(x,y,z)
由
取x=1,得y=-
,z=
,∴
=(1,-
,
)
依题意有cos
=
,⇒2λ2+λ-1=0
解得λ=-1(舍去)或λ=
∴当点F在AB中点时,恰好满足题意.
 (Ⅰ)证明:连CE交BD于点M,∵四边形BCDE是矩形,M为CE中点,
(Ⅰ)证明:连CE交BD于点M,∵四边形BCDE是矩形,M为CE中点,在△ACE中,G为AE中点,故GM∥AC.
∵GM?平面BDG,AC?平面BDG,∴AC∥平面BDG.
(Ⅱ)解:取BC中点O,分别以OB,OM,OA所在的直线为x,y,z轴建立空间直角坐标系,则A(0,0,
| 3 |
| 2 |
| BF |
| BA |
| 3 |
设平面CEF的法向量为
| n |
由
|
取x=1,得y=-
| 2 |
| λ-2 | ||
|
| n |
| 2 |
| λ-2 | ||
|
依题意有cos
| π |
| 4 |
|
| ||||||
|
解得λ=-1(舍去)或λ=
| 1 |
| 2 |
∴当点F在AB中点时,恰好满足题意.
点评:本题主要考查直线和平面平行的判定定理,以及利用向量法解决二面角的大小问题,综合性较强,运算量较大.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE(A′∉平面ABC)是△ADE绕DE旋转过程中的一个图形,有下列命题:
如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE(A′∉平面ABC)是△ADE绕DE旋转过程中的一个图形,有下列命题: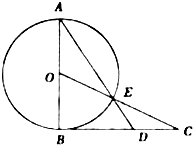 如图,AB为⊙O的直径,过点B作⊙O的切线BC,OC交⊙O于点E,AE的延长线交BC于点D.
如图,AB为⊙O的直径,过点B作⊙O的切线BC,OC交⊙O于点E,AE的延长线交BC于点D.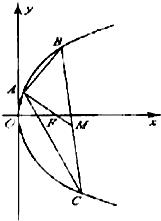 已知点A(2,8),B(x1,y1),C(x2,y2)在抛物线y2=2px,(p>0)上,△ABC的重心与此抛物线的焦点F重合(如图)
已知点A(2,8),B(x1,y1),C(x2,y2)在抛物线y2=2px,(p>0)上,△ABC的重心与此抛物线的焦点F重合(如图)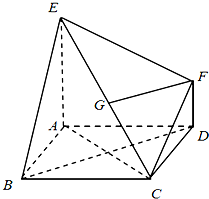 如图,已知多面体EABCDF的底面ABCD是正方形,EA⊥底面ABCD,FD∥EA,且EA=2FD.
如图,已知多面体EABCDF的底面ABCD是正方形,EA⊥底面ABCD,FD∥EA,且EA=2FD. 如图,在△ABC中,AB=4,AC=1,∠BAC=60°.
如图,在△ABC中,AB=4,AC=1,∠BAC=60°. 如图,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的中点,求证:PO∥面D1BQ.
如图,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的中点,求证:PO∥面D1BQ.