题目内容
已知：如图AD，BC，AE分别是⊙O的三条切线，切点分别是D，E，F，AG是⊙O的一条割线，交⊙O于F，G两点，△ABC的周长2| 3 |
（1）求证：AF•AG=3；
（2）求AF2+FG2的最大值．
考点：与圆有关的比例线段
专题：选作题,立体几何
分析：（1）先证明AD=AE，再利用切割线定理，即可证明AF•AG=3；
（2）设AF=x，表示出AF2+FG2，结合AF=x∈[1，
)，即可求AF2+FG2的最大值．
（2）设AF=x，表示出AF2+FG2，结合AF=x∈[1，
| 3 |
解答：
（1）证明：△ABC的周长2
，得到AB+AC+BF+CF=2
，
又因为：BF=BD，CF=CE，所以AD+AE=2
，
因为：AD=AE，所以AD=AE=
．
所以AF•AG=AD2=
2=3．--------------（5分）
（2）解：设AF=x，则AG=
，FG=x-
，
所以AF2+FG2=2x2+
-6，
因为⊙O的半径为1，得到AF=x∈[1，
)，
所以AF2+FG2的最大值为5．--------------（10分）
| 3 |
| 3 |
又因为：BF=BD，CF=CE，所以AD+AE=2
| 3 |
因为：AD=AE，所以AD=AE=
| 3 |
所以AF•AG=AD2=
| 3 |
（2）解：设AF=x，则AG=
| 3 |
| x |
| 3 |
| x |
所以AF2+FG2=2x2+
| 9 |
| x2 |
因为⊙O的半径为1，得到AF=x∈[1，
| 3 |
所以AF2+FG2的最大值为5．--------------（10分）
点评：本题考查切割线定理，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
如图，该程序运行后的输出结果为（ ）
| A、0 | B、3 | C、12 | D、-2 |
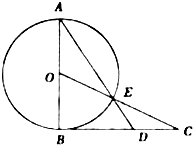如图，AB为⊙O的直径，过点B作⊙O的切线BC，OC交⊙O于点E，AE的延长线交BC于点D．
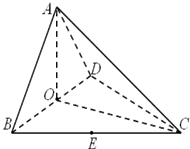（Ⅰ）求证：AO⊥平面BCD；
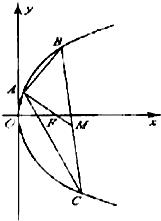已知点A（2，8），B（x1，y1），C（x2，y2）在抛物线y2=2px，（p＞0）上，△ABC的重心与此抛物线的焦点F重合（如图）
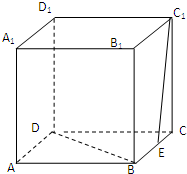在正方体ABCD-A1B1C1D1中，E为BC的中点，求：