题目内容
已知函数f(x)=|2x-1|+|2x-3|,x∈R.
(1)解不等式f(x)≤5;
(2)若不等式m2-m<f(x),?x∈R都成立,求实数m的取值范围.
(1)解不等式f(x)≤5;
(2)若不等式m2-m<f(x),?x∈R都成立,求实数m的取值范围.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(1)原不等式等价于
①,或
②,或
③.分别求得①、②、③的解集,再取并集,即得所求.
(2)利用绝对值三角不等式求得f(x)的最小值为2,可得 m2-m<2,由此解得实数m的取值范围.
|
|
|
(2)利用绝对值三角不等式求得f(x)的最小值为2,可得 m2-m<2,由此解得实数m的取值范围.
解答:
解:(1)原不等式等价于
①,或
②,或
③.
解①求得-
≤x<
,解②求得
≤x≤
,解③求得
<x≤
,
因此不等式的解集为[-
,
].
(2)∵f(x)=|2x-1|+|2x-3|≥|2x-1-(2x-3)|=2,
∴m2-m<2,解得-1<m<2,
即实数m的取值范围为(-1,2).
|
|
|
解①求得-
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
| 4 |
因此不等式的解集为[-
| 1 |
| 4 |
| 9 |
| 4 |
(2)∵f(x)=|2x-1|+|2x-3|≥|2x-1-(2x-3)|=2,
∴m2-m<2,解得-1<m<2,
即实数m的取值范围为(-1,2).
点评:本题主要考查绝对值三角不等式的应用,绝对值不等式的解法,体现了转化、分类讨论的数学思想,属于基础题.

练习册系列答案
相关题目
如图,该程序运行后的输出结果为( )


| A、0 | B、3 | C、12 | D、-2 |
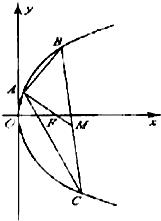 已知点A(2,8),B(x1,y1),C(x2,y2)在抛物线y2=2px,(p>0)上,△ABC的重心与此抛物线的焦点F重合(如图)
已知点A(2,8),B(x1,y1),C(x2,y2)在抛物线y2=2px,(p>0)上,△ABC的重心与此抛物线的焦点F重合(如图) 如图,在△ABC中,AB=4,AC=1,∠BAC=60°.
如图,在△ABC中,AB=4,AC=1,∠BAC=60°.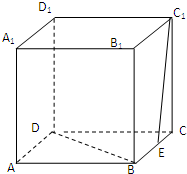 在正方体ABCD-A1B1C1D1中,E为BC的中点,求:
在正方体ABCD-A1B1C1D1中,E为BC的中点,求: