题目内容
求函数y=sin（2x+
）cos（2x+
）的最值，周期及单调减区间．
| π |
| 6 |
| π |
| 6 |
考点：两角和与差的正弦函数,三角函数的周期性及其求法,正弦函数的单调性,三角函数的最值
专题：三角函数的求值
分析：由两角和与差的三角函数公式和及二倍角公式化简已知函数可得y=
sin（4x+
），易得答案．
| 1 |
| 2 |
| π |
| 3 |
解答：
解：化简可得y=sin（2x+
）cos（2x+
）=
sin（4x+
）
∴函数的最大值为
，最小值为-
，
周期T=
=
，
由2kπ+
≤4x+
≤2kπ+
解得
+
≤x≤
+
，
∴函数的单调减区间为：[
+
，
+
]，k∈Z
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
| π |
| 3 |
∴函数的最大值为
| 1 |
| 2 |
| 1 |
| 2 |
周期T=
| 2π |
| 4 |
| π |
| 2 |
由2kπ+
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
| kπ |
| 2 |
| π |
| 24 |
| kπ |
| 2 |
| 7π |
| 24 |
∴函数的单调减区间为：[
| kπ |
| 2 |
| π |
| 24 |
| kπ |
| 2 |
| 7π |
| 24 |
点评：本题考查两角和与差的三角函数公式，涉及三角函数的单调性和周期性以及二倍角公式，属中档题．
练习册系列答案
华东师大版一课一练系列答案
相关题目
正三角形ABC中，D，E分别是AB，AC的中点，则以B，C为焦点且过D，E的双曲线的离心率是（ ）
A、
| ||||
B、
| ||||
C、2
| ||||
D、
|
若z1=a+2i，z2=3-4i，且
为纯虚数，则实数a的值是（ ）
| z1 |
| z2 |
| A、2 | ||
B、
| ||
C、
| ||
| D、3 |
如图，该程序运行后的输出结果为（ ）
| A、0 | B、3 | C、12 | D、-2 |
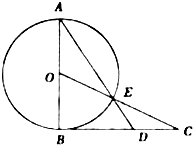如图，AB为⊙O的直径，过点B作⊙O的切线BC，OC交⊙O于点E，AE的延长线交BC于点D．
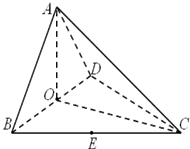（Ⅰ）求证：AO⊥平面BCD；
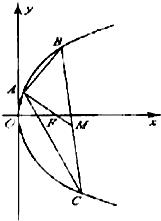已知点A（2，8），B（x1，y1），C（x2，y2）在抛物线y2=2px，（p＞0）上，△ABC的重心与此抛物线的焦点F重合（如图）