题目内容
直线l过点A(2,4)且与圆x2+y2=4相切,则l的方程是( )
| A、3x-4y+10=0 |
| B、x=2或3x-4y+10=0 |
| C、x-y+2=0 |
| D、x=2或x-y+2=0 |
考点:圆的切线方程
专题:直线与圆
分析:当斜率不存在时,根据直线和圆相切求得切线方程;当斜率存在时,根据圆心到切线的距离等于半径,求得斜率k的值,从而求得切线l的方程.
解答:
解:当切线的斜率不存在时,圆x2+y2=4的切线l的方程是x=2,
当切线的斜率存在时,设切线方程为y-4=k(x-2),即 kx-y+4-2k=0,
由圆心到切线的距离等于半径可得
=2,求得k=
,故圆的切线方程为 3x-4y+10=0,
综上可得,圆的切线方程为 x=2,或3x-4y+10=0,
故选:B.
当切线的斜率存在时,设切线方程为y-4=k(x-2),即 kx-y+4-2k=0,
由圆心到切线的距离等于半径可得
| |0-0+4-2k| | ||
|
| 3 |
| 4 |
综上可得,圆的切线方程为 x=2,或3x-4y+10=0,
故选:B.
点评:本题主要考查直线和圆相切的性质,体现了转化、分类讨论的数学思想,属于基础题.

练习册系列答案
相关题目
正三角形ABC中,D,E分别是AB,AC的中点,则以B,C为焦点且过D,E的双曲线的离心率是( )
A、
| ||||
B、
| ||||
C、2
| ||||
D、
|
函数f(x)=(x2-2)(x2-3x+2)的零点个数为( )
| A、1 | B、2 | C、3 | D、4 |
 如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE(A′∉平面ABC)是△ADE绕DE旋转过程中的一个图形,有下列命题:
如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE(A′∉平面ABC)是△ADE绕DE旋转过程中的一个图形,有下列命题:①平面A′FG⊥平面ABC;
②BC∥平面A′DE;
③三棱锥A′-DEF的体积最大值为
| 1 |
| 64 |
④存在某个位置,使得DF与A′E垂直.
其中正确的命题是( )
| A、② | B、②③ |
| C、①②③ | D、①②③④ |
若z1=a+2i,z2=3-4i,且
为纯虚数,则实数a的值是( )
| z1 |
| z2 |
| A、2 | ||
B、
| ||
C、
| ||
| D、3 |
如图,该程序运行后的输出结果为( )


| A、0 | B、3 | C、12 | D、-2 |
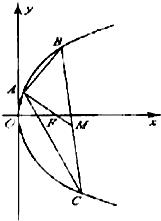 已知点A(2,8),B(x1,y1),C(x2,y2)在抛物线y2=2px,(p>0)上,△ABC的重心与此抛物线的焦点F重合(如图)
已知点A(2,8),B(x1,y1),C(x2,y2)在抛物线y2=2px,(p>0)上,△ABC的重心与此抛物线的焦点F重合(如图)