题目内容
已知函数y=f(x)(x∈R)不恒为零,且对于任意实数x1,x2,都有f(x1x2)=x1f(x2)+x2f(x1).若f(x)是以3为周期的周期函数,在区间(-6,6)内方程f(x)=0有且只有15个根,并且最大的根是x=5,求方程f(x)=0在区间(-6,6)内所有的根.
考点:抽象函数及其应用
专题:转化思想,函数的性质及应用
分析:利用赋值法先由条件“对于任意实数x1,x2,都有f(x1x2)=x1f(x2)+x2f(x1)”得出隐含条件f(x)是奇函数,再结合3为周期,反复利用两个性质得出所有的根.
解答:
解:∵对于任意实数x1,x2,都有f(x1x2)=x1f(x2)+x2f(x1),令x1=x2=1得f(1)=0,
再令x1=x2=-1得f(1)=-2f(-1)=0,∴f(-1)=0,
再令x1=-1,x2=x代入得f(-x)=-f(x)+xf(-1)=-f(x),∴函数y=f(x)是奇函数,
又∵x∈R,∴f(0)=0;所以0,-1,1是f(x)=0的根,结合f(x)以3为周期,且是奇函数,
则f(-1)=f(1)=f(-4)=f(4)=0,f(0)=f(3)=f(-3)=0,由已知f(5)=0,∴f(-5)=f(-2)=f(2)=0,
∴f(1)=f(2×
)=2f(
)+
f(2)=0,∴f(
)=0,同理f(
)=f(
)=f(
)=0,又∵在区间(-6,6)内方程f(x)=0有且只有15个根,
∴方程f(x)=0在区间(-6,6)内的根为:0,-1,1,-2,2,-3,3,-4,4,-5,5,
,
,
,
,共15个.
再令x1=x2=-1得f(1)=-2f(-1)=0,∴f(-1)=0,
再令x1=-1,x2=x代入得f(-x)=-f(x)+xf(-1)=-f(x),∴函数y=f(x)是奇函数,
又∵x∈R,∴f(0)=0;所以0,-1,1是f(x)=0的根,结合f(x)以3为周期,且是奇函数,
则f(-1)=f(1)=f(-4)=f(4)=0,f(0)=f(3)=f(-3)=0,由已知f(5)=0,∴f(-5)=f(-2)=f(2)=0,
∴f(1)=f(2×
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
∴方程f(x)=0在区间(-6,6)内的根为:0,-1,1,-2,2,-3,3,-4,4,-5,5,
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
点评:这个题以抽象函数为载体,利用赋值法推出其奇函数的性质,然后将周期性与奇偶性相结合,反复利用、转换,直到求出所有的值,有一定难度.

练习册系列答案
相关题目
 给出四个函数图象分别满足:
给出四个函数图象分别满足:①f(x+y)=f(x)+f(y);
②g(x+y)=g(x)•g(y);
③u(x•y)=u(x)+u(y);
④v(x•y)=v(x)•v(y).
与如图函数图象对应的是( )
| A、①-a,②-b,③-c,④-d |
| B、①-b,②-c,③-a,④-d |
| C、①-a,②-c,③-b,④-d |
| D、①-d,②-a,③-b,④-c |
已知直线l的方程:x-y-1=0,则直线l的倾斜角α=( )
| A、45° | B、60° |
| C、120° | D、135° |
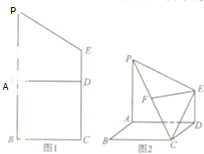 如图1在梯形PBCE中,PB=2BC=4,CE=3,A是线段PB上一点,AD∥BC,现将四边形PADE沿AD折起,使得平面PADE⊥平面ABCD,连接PC,CE,得到如图2所示的空间图形,已知F是PC的中点,EF∥平面ABCD.
如图1在梯形PBCE中,PB=2BC=4,CE=3,A是线段PB上一点,AD∥BC,现将四边形PADE沿AD折起,使得平面PADE⊥平面ABCD,连接PC,CE,得到如图2所示的空间图形,已知F是PC的中点,EF∥平面ABCD. 如图,在菱形ABCD中,AB=BD=2,三角形PAD为等边三角形.将它沿AD折成大小为α(
如图,在菱形ABCD中,AB=BD=2,三角形PAD为等边三角形.将它沿AD折成大小为α(