题目内容
已知a,b,c都是正数,求证:
(1)
+
+
≥a+b+c;
(2)
+
+
≥
+
+
.
(1)
| a2 |
| b |
| b2 |
| c |
| c2 |
| a |
(2)
| 1 |
| 2a |
| 1 |
| 2b |
| 1 |
| 2c |
| 1 |
| b+c |
| 1 |
| c+a |
| 1 |
| a+b |
考点:不等式的证明
专题:选作题,不等式
分析:(1)利用b+
≥2a,c+
≥2b,a+
≥2c,三个式子相加可得结论;
(2)该题是轮换式不等式的证明,可以利用基本不等式证
(
+
)≥
≥
;
(
+
)≥
≥
;
(
+
)≥
≥
,将三式相加可证得结论.
| a2 |
| b |
| b2 |
| c |
| c2 |
| a |
(2)该题是轮换式不等式的证明,可以利用基本不等式证
| 1 |
| 2 |
| 1 |
| 2a |
| 1 |
| 2b |
| 1 | ||
2
|
| 1 |
| a+b |
| 1 |
| 2 |
| 1 |
| 2b |
| 1 |
| 2c |
| 1 | ||
2
|
| 1 |
| b+c |
| 1 |
| 2 |
| 1 |
| 2c |
| 1 |
| 2a |
| 1 | ||
2
|
| 1 |
| c+a |
解答:
证明:(1)∵a,b,c都是正数,
∴b+
≥2a,c+
≥2b,a+
≥2c,
三个式子相加可得b+
+c+
+a+
≥2a+2b+2c,
∴
+
+
≥a+b+c;
(2)∵a、b、c均为正实数,
∴
(
+
)≥
≥
,当a=b时等号成立;
(
+
)≥
≥
,当b=c时等号成立;
(
+
)≥
≥
,当a=c时等号成立;
三个不等式相加即得
+
+
≥
+
+
,
当且仅当a=b=c时等号成立.
∴b+
| a2 |
| b |
| b2 |
| c |
| c2 |
| a |
三个式子相加可得b+
| a2 |
| b |
| b2 |
| c |
| c2 |
| a |
∴
| a2 |
| b |
| b2 |
| c |
| c2 |
| a |
(2)∵a、b、c均为正实数,
∴
| 1 |
| 2 |
| 1 |
| 2a |
| 1 |
| 2b |
| 1 | ||
2
|
| 1 |
| a+b |
| 1 |
| 2 |
| 1 |
| 2b |
| 1 |
| 2c |
| 1 | ||
2
|
| 1 |
| b+c |
| 1 |
| 2 |
| 1 |
| 2c |
| 1 |
| 2a |
| 1 | ||
2
|
| 1 |
| c+a |
三个不等式相加即得
| 1 |
| 2a |
| 1 |
| 2b |
| 1 |
| 2c |
| 1 |
| b+c |
| 1 |
| c+a |
| 1 |
| a+b |
当且仅当a=b=c时等号成立.
点评:本题主要考查了不等式的证明,以及基本不等式的应用,同时考查了分析问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知a=
(
cosx-sinx)dx,则二项式(x2+
)5展开式中第三项的系数为( )
| ∫ | π 0 |
| 3 |
| a |
| x |
| A、80 | B、-80 |
| C、-40 | D、40 |
已知非零向量
,
,
满足
+
+
=0,向量
与
的夹角为60°,且|
|=|
|=1,则向量
与
的夹角为( )
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| a |
| c |
| A、30° | B、60° |
| C、120° | D、150° |
将4名学生分到三个不同的班级,在每个班级至少分到一名学生的条件下,其中甲、乙两名学生不能分到同一个班级的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
曲线y=2x-x3在横坐标为-1的点处的切线为l,则直线l的方程为( )
| A、x+y+2=0 |
| B、x-y=0 |
| C、x-y-2=0 |
| D、x+y-2=0 |
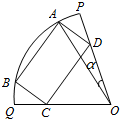 已知OPQ是半径为1,圆心角为2θ(θ为定值)的扇形,A是扇形弧上的动点,四边形ABCD是扇形内的内接矩形,记∠AOP=α(0<α<θ).
已知OPQ是半径为1,圆心角为2θ(θ为定值)的扇形,A是扇形弧上的动点,四边形ABCD是扇形内的内接矩形,记∠AOP=α(0<α<θ).