题目内容
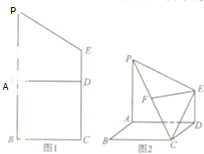 如图1在梯形PBCE中,PB=2BC=4,CE=3,A是线段PB上一点,AD∥BC,现将四边形PADE沿AD折起,使得平面PADE⊥平面ABCD,连接PC,CE,得到如图2所示的空间图形,已知F是PC的中点,EF∥平面ABCD.
如图1在梯形PBCE中,PB=2BC=4,CE=3,A是线段PB上一点,AD∥BC,现将四边形PADE沿AD折起,使得平面PADE⊥平面ABCD,连接PC,CE,得到如图2所示的空间图形,已知F是PC的中点,EF∥平面ABCD.(Ⅰ)求DE的长;
(Ⅱ)求点A到平面PCE的距离.
考点:点、线、面间的距离计算,与二面角有关的立体几何综合题
专题:空间位置关系与距离
分析:(Ⅰ)连结AC,BD交于点O,连结OF,则OF∥PA,且OF=
PA,又知DE∥PA,推断出DE∥OF,根据EF∥平面ABCD,平面ODEF∩平面ABCD=OD,判断出EF∥OD,进而可知四边形ODEF为平行四边形,求得DE=
PA,又PA+CD=4,CD+DE=3,则DE可求.
(Ⅱ)由EF∥BD,BD⊥平面PAC,根据线面垂直的判定知EF⊥平面PAC,过点A作AG⊥PC,垂足为G,则AG⊥平面PCE,继而求得AG,即点A到平面PCE的距离.
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)由EF∥BD,BD⊥平面PAC,根据线面垂直的判定知EF⊥平面PAC,过点A作AG⊥PC,垂足为G,则AG⊥平面PCE,继而求得AG,即点A到平面PCE的距离.
解答:
解:(Ⅰ)连结AC,BD交于点O,连结OF,则OF∥PA,且OF=
PA,
又DE∥PA,
∴DE∥OF,
∵EF∥平面ABCD,平面ODEF∩平面ABCD=OD,
∴EF∥OD,
∴四边形ODEF为平行四边形,
∴DE=
PA,
又PA+CD=4,CD+DE=3,
∴DE=1.
(Ⅱ)∵EF∥BD,BD⊥平面PAC,
∴EF⊥平面PAC,
过点A作AG⊥PC,垂足为G,则AG⊥平面PCE,
AG=
=
,即点A到平面PCE的距离为
.
| 1 |
| 2 |
又DE∥PA,
∴DE∥OF,
∵EF∥平面ABCD,平面ODEF∩平面ABCD=OD,
∴EF∥OD,
∴四边形ODEF为平行四边形,
∴DE=
| 1 |
| 2 |
又PA+CD=4,CD+DE=3,
∴DE=1.
(Ⅱ)∵EF∥BD,BD⊥平面PAC,
∴EF⊥平面PAC,
过点A作AG⊥PC,垂足为G,则AG⊥平面PCE,
AG=
2×2
| ||
|
2
| ||
| 3 |
2
| ||
| 3 |
点评:本题主要考查了线面平行和线面垂直判定定理的应用,点到面的距离.考查了学生综合运用所学知识的能力.

练习册系列答案
相关题目
调查某市出租车使用年限x和该年支出维修费用y(万元),得到数据如下:
则回归方程
=
x+
,必过定点( )
| 使用年限x | 2 | 3 | 4 | 5 | 6 |
| 维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
 |
| y |
 |
| b |
 |
| a |
| A、(2,3) |
| B、(3,4) |
| C、(4,5) |
| D、(5,6) |
曲线y=2x-x3在横坐标为-1的点处的切线为l,则直线l的方程为( )
| A、x+y+2=0 |
| B、x-y=0 |
| C、x-y-2=0 |
| D、x+y-2=0 |
 某工厂生产A、B两种产品,计划每种产品的生产量不少于15千克,已知生产A产品1千克要用煤9吨,电力4千瓦,3个工作日;生产B产品1千克要用煤4吨,电力5千瓦,10个工作日.又知生产出A产品1千克可获利7万元,生产出B产品1千克可获利12万元,现在工厂只有煤360吨,电力200千瓦,300个工作日,
某工厂生产A、B两种产品,计划每种产品的生产量不少于15千克,已知生产A产品1千克要用煤9吨,电力4千瓦,3个工作日;生产B产品1千克要用煤4吨,电力5千瓦,10个工作日.又知生产出A产品1千克可获利7万元,生产出B产品1千克可获利12万元,现在工厂只有煤360吨,电力200千瓦,300个工作日,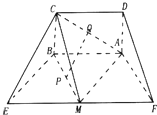 如图,四边形ABEF是等腰梯形,AB∥EF,AF=BE=2,EF=4
如图,四边形ABEF是等腰梯形,AB∥EF,AF=BE=2,EF=4