题目内容
已知函数f(x)=
x2-(a+3)x+3alnx,(a∈R).
(1)若f(x)的图象在x=1处的切线为l:y=b,求a,b的值及f(x)的单调区间;
(2)对于定义在正实数集R+上的函数S(x),T(x),若对任意x2>x1>0,均有S(x2)-S(x1)>k[T(x2)-T(x1)],(k∈R+),则称函数S(x)是T(x)的“超k倍速”函数,已知函数f(x)是g(x)=-x,(x∈R+)的“超3倍速”函数,求a的取值范围.
| 1 |
| 2 |
(1)若f(x)的图象在x=1处的切线为l:y=b,求a,b的值及f(x)的单调区间;
(2)对于定义在正实数集R+上的函数S(x),T(x),若对任意x2>x1>0,均有S(x2)-S(x1)>k[T(x2)-T(x1)],(k∈R+),则称函数S(x)是T(x)的“超k倍速”函数,已知函数f(x)是g(x)=-x,(x∈R+)的“超3倍速”函数,求a的取值范围.
考点:利用导数研究曲线上某点切线方程,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(1)求出原函数的导函数,得到函数在x=1时的导数值,由导数值等于0求得a的值;
(2)利用题目给出的新定义,得到对?x2>x1>0有f(x2)-f(x1)>3(x1-x2),即f(x2)+3x2>
f(x1)+3x1,构造函数g(x)=f(x)+3x,问题转化为g(x)在(0,+∞)上是增函数,也就是g′(x)≥0
在(0,+∞)上恒成立,然后分类分析,求出导函数的最小值,由最小值大于等于0求得a的范围.
(2)利用题目给出的新定义,得到对?x2>x1>0有f(x2)-f(x1)>3(x1-x2),即f(x2)+3x2>
f(x1)+3x1,构造函数g(x)=f(x)+3x,问题转化为g(x)在(0,+∞)上是增函数,也就是g′(x)≥0
在(0,+∞)上恒成立,然后分类分析,求出导函数的最小值,由最小值大于等于0求得a的范围.
解答:
解:由f(x)=
x2-(a+3)x+3alnx,
得:f′(x)=x-(a+3)+
,
∵若f(x)的图象在x=1处的切线为l:y=b,
∴f′(1)=2a-2=0,解得a=1.
∴b=f(1)=-
.
于是,f′(x)=x-4+
=
(x>0).
则x∈(0,1)∪(3,+∞)时,f′(x)>0,
x∈(1,3)时,f′(x)<0.
故f(x)的单调递增区间是(0,1),(3,+∞),
单调减区间是(1,3);
(2)∵f(x)是g(x)的“超3倍速函数”
∴对?x2>x1>0有f(x2)-f(x1)>3(x1-x2),
即f(x2)+3x2>f(x1)+3x1,
也就是g(x)=f(x)+3x在(0,+∞)上是增函数,
由于g′(x)=x-a+
,
于是对?x>0,g′(x)≥0恒成立.
令h(x)=g′(x)=x-a+
①当a<0时,显然h(x)在(0,+∞)上是增函数
且x→0,h(x)→-∞,不合题意;
②当a=0时,
对?x>0,h(x)=x>0符合题意;
③当a>0时,
h(x)=x+
-a≥2
-a(当且仅当x=
时等号成立).
∴2
-a≥0,
得0<a≤12.
综上得a的取值范围是:0≤a≤12.
| 1 |
| 2 |
得:f′(x)=x-(a+3)+
| 3a |
| x |
∵若f(x)的图象在x=1处的切线为l:y=b,
∴f′(1)=2a-2=0,解得a=1.
∴b=f(1)=-
| 7 |
| 2 |
于是,f′(x)=x-4+
| 3 |
| x |
| (x-3)(x-1) |
| x |
则x∈(0,1)∪(3,+∞)时,f′(x)>0,
x∈(1,3)时,f′(x)<0.
故f(x)的单调递增区间是(0,1),(3,+∞),
单调减区间是(1,3);
(2)∵f(x)是g(x)的“超3倍速函数”
∴对?x2>x1>0有f(x2)-f(x1)>3(x1-x2),
即f(x2)+3x2>f(x1)+3x1,
也就是g(x)=f(x)+3x在(0,+∞)上是增函数,
由于g′(x)=x-a+
| 3a |
| x |
于是对?x>0,g′(x)≥0恒成立.
令h(x)=g′(x)=x-a+
| 3a |
| x |
①当a<0时,显然h(x)在(0,+∞)上是增函数
且x→0,h(x)→-∞,不合题意;
②当a=0时,
对?x>0,h(x)=x>0符合题意;
③当a>0时,
h(x)=x+
| 3a |
| x |
| 3a |
| 3a |
∴2
| 3a |
得0<a≤12.
综上得a的取值范围是:0≤a≤12.
点评:本题考查了利用导数研究曲线上某点处的切线方程,考查了利用导数研究函数的单调性,考查了数学转化思想方法及分类讨论的数学思想方法,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若等比数列{an}满足2a4=a6-a5,则q=( )
| A、-1或2 | B、1或-2 |
| C、0 | D、-1或-2 |
将4名学生分到三个不同的班级,在每个班级至少分到一名学生的条件下,其中甲、乙两名学生不能分到同一个班级的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
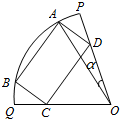 已知OPQ是半径为1,圆心角为2θ(θ为定值)的扇形,A是扇形弧上的动点,四边形ABCD是扇形内的内接矩形,记∠AOP=α(0<α<θ).
已知OPQ是半径为1,圆心角为2θ(θ为定值)的扇形,A是扇形弧上的动点,四边形ABCD是扇形内的内接矩形,记∠AOP=α(0<α<θ). 设四边形ABCD内接于圆O,其对边AD与BC的延长线交于圆O外一点E,自E引一直线平行于AC,交BD延长线于点M,自M引MT切圆O于T点,则MT=ME.
设四边形ABCD内接于圆O,其对边AD与BC的延长线交于圆O外一点E,自E引一直线平行于AC,交BD延长线于点M,自M引MT切圆O于T点,则MT=ME.