题目内容
 如图,在菱形ABCD中,AB=BD=2,三角形PAD为等边三角形.将它沿AD折成大小为α(
如图,在菱形ABCD中,AB=BD=2,三角形PAD为等边三角形.将它沿AD折成大小为α(| π |
| 2 |
(Ⅰ)证明:AD⊥PB;
(Ⅱ)当α为何值时,二面角P-CD-A的平面角的正切值大小为2
| 3 |
考点:与二面角有关的立体几何综合题
专题:空间角
分析:(Ⅰ)取AD的中点E,连结PE,BE,由已知条件推导出AD⊥PE,AD⊥BE,由此能证明AD⊥平面PEB,从而得到AD⊥PB.
(Ⅱ)过点P在平面PEB内作BE的垂线,垂足为F,由已知条件得到∠PEB为所折成二面角的平面角α的补角,
∠PEB=π-α,PE=
,EF=-
cosα,PF=
sinα,过F在平面ABD内作FG⊥CD,垂足为G,连结PG,则∠PGF为二面角P-CD-A的平面角,由此能求出结果.
(Ⅱ)过点P在平面PEB内作BE的垂线,垂足为F,由已知条件得到∠PEB为所折成二面角的平面角α的补角,
∠PEB=π-α,PE=
| 3 |
| 3 |
| 3 |
解答:
(Ⅰ)证明:取AD的中点E,连结PE,BE,
∵△PAD与△ABD为等边三角形,
∴AD⊥PE,AD⊥BE,PE∩BE=E,
∴AD⊥平面PEB,
∴AD⊥PB.
(Ⅱ)解:过点P在平面PEB内作BE的垂线,垂足为F,
由(Ⅰ)知面PEB⊥面ADB,∴PF⊥平面ABD,
由(Ⅰ)知∠PEB为所折成二面角的平面角α的补角,
∠PEB=π-α,
PE=
,EF=-
cosα,PF=
sinα,
过F在平面ABD内作FG⊥CD,垂足为G,连结PG,
则∠PGF为二面角P-CD-A的平面角,
在平面图形FBCG中,延长BF,CD相交于H,
由题意知FG=
,
∴tan∠PGF=
=2
,
∴sinα-
cosα=
,
∴sin(α-
)=
,
∴α=
.
∵△PAD与△ABD为等边三角形,
∴AD⊥PE,AD⊥BE,PE∩BE=E,
∴AD⊥平面PEB,
∴AD⊥PB.
(Ⅱ)解:过点P在平面PEB内作BE的垂线,垂足为F,
由(Ⅰ)知面PEB⊥面ADB,∴PF⊥平面ABD,
由(Ⅰ)知∠PEB为所折成二面角的平面角α的补角,

∠PEB=π-α,
PE=
| 3 |
| 3 |
| 3 |
过F在平面ABD内作FG⊥CD,垂足为G,连结PG,
则∠PGF为二面角P-CD-A的平面角,
在平面图形FBCG中,延长BF,CD相交于H,
由题意知FG=
| ||||
| 2 |
∴tan∠PGF=
| ||||
|
| 3 |
∴sinα-
| 3 |
| 3 |
∴sin(α-
| π |
| 3 |
| ||
| 2 |
∴α=
| 2π |
| 3 |
点评:本题考查异面直线垂直的证明,考查角的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
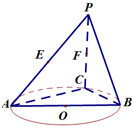 如图,AB是圆O的直径,点C是圆O上异于A,B的点,直线PC⊥平面ABC,E,F分别是PA,PC的中点.
如图,AB是圆O的直径,点C是圆O上异于A,B的点,直线PC⊥平面ABC,E,F分别是PA,PC的中点.