题目内容
已知函数f(x)=x2+
(x≠0,a∈R),若函数f(x)在x∈[3,+∞)上是增函数,求a的最大值.
| a |
| x |
考点:函数单调性的性质
专题:函数的性质及应用,导数的综合应用
分析:根据题意,对f(x)求导,在x∈[3,+∞)上,f′(x)≥0恒成立;由此求出a的最大值即可.
解答:
解:∵f(x)=x2+
(x≠0,a∈R),
∴f′(x)=2x-
=
;
又∵f(x)在x∈[3,+∞)上是增函数,
∴当x≥3时,f′(x)≥0恒成立;
即2x3-a≥0,
∴a≤2x3;
又x=3时,2x3取得最小值2×33=54,
∴a≤54;
即a的最大值是54.
| a |
| x |
∴f′(x)=2x-
| a |
| x2 |
| 2x3-a |
| x2 |
又∵f(x)在x∈[3,+∞)上是增函数,
∴当x≥3时,f′(x)≥0恒成立;
即2x3-a≥0,
∴a≤2x3;
又x=3时,2x3取得最小值2×33=54,
∴a≤54;
即a的最大值是54.
点评:本题考查了利用导数研究函数的性质以及求函数最值的问题,解题时应灵活应用导数判断函数的单调性和求最值,是中档题.

练习册系列答案
相关题目
从正六边形六个顶点及其中心这7个点中,任取两个点,则这两个点的距离大于该正六边形边长的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
抛物线x2+y=0的焦点坐标是( )
A、(0,-
| ||
B、(0,
| ||
C、(
| ||
D、(-
|
一个三角形的两个内角为45°和30°,如果45°角所对的边长是则30°角所对的边长为( )
A、2
| ||
B、3
| ||
C、
| ||
D、3
|
记S=1!+2!+3!+…+99!,则S的个位数字是( )
| A、9 | B、5 | C、3 | D、0 |
 在正方形ABCD-A1B1C1D1中,G,H分别是B1C1,C1D1的中点.
在正方形ABCD-A1B1C1D1中,G,H分别是B1C1,C1D1的中点.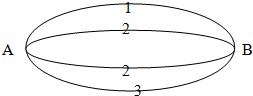 如图A、B两点之间有4条网线并联,他们能通过的最大信息量分别为1、2、2、3,现从中任取三条网线且使每条网线通过最大信息量;
如图A、B两点之间有4条网线并联,他们能通过的最大信息量分别为1、2、2、3,现从中任取三条网线且使每条网线通过最大信息量;