题目内容
判断函数f（x）=x+
在（-1，0）上的单调性．
| 1 |
| x |
考点：函数单调性的判断与证明
专题：函数的性质及应用
分析：利用函数的单调性定义进行判断即可．
解答：
解：任取x1、x2∈（-1，0），且x1＜x2；
则f（x1）-f（x2）=（x1+
）-（x2+
）=
，
∵-1＜x1＜x2＜0，
∴x1-x2＜0，x1x2-1＜0，x1x2＞0；
∴f（x1）-f（x2）＞0，即f（x1）＜f（x2）；
∴f（x）在（-1，0）上是减函数．
则f（x1）-f（x2）=（x1+
| 1 |
| x1 |
| 1 |
| x2 |
| (x1-x2)(x1x2-1) |
| x1x2 |
∵-1＜x1＜x2＜0，
∴x1-x2＜0，x1x2-1＜0，x1x2＞0；
∴f（x1）-f（x2）＞0，即f（x1）＜f（x2）；
∴f（x）在（-1，0）上是减函数．
点评：本题考查了函数的单调性问题，解题时可以利用单调性定义进行判断，是基础题．
练习册系列答案
相关题目
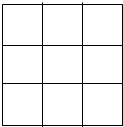将大小形状相同的4个红球和2个白球放入如图所示的九宫格中，每格至多放一个，要求相邻方格的小球不同色（有公共边的两个方格为相邻），则所有不同的放法种数为（ ）设f（x）是定义在R上的奇函数，且f（2）=0，当x＞0时，有
＞0恒成立，则不等式f（x）＞0的解集是（ ）
| xf′(x)-f(x) |
| x2 |
| A、（-∞，-2）∪（2，+∞） |
| B、（-2，0）∪（0，2） |
| C、（-2，0）∪（2，+∞） |
| D、（-∞，-2）∪（0，2） |