题目内容
已知函数f(x)的定义域为R,y=f(x-2)是偶函数,且f(x)在[-4,-2]上是增函数,则f(-3.5),f(-1),f(0)的大小关系为 .
考点:奇偶性与单调性的综合
专题:计算题,函数的性质及应用
分析:确定f(-3.5)=f(1.5-2)=f(-0.5),函数f(x)在[-2,0]上是减函数,即可得出结论.
解答:
解:∵函数y=f(x-2)为偶函数,∴图象关于x=0对称,f(-3.5)=f(1.5-2)=f(-0.5)
又∵由y=f(x-2)向左平移2个单位可得函数y=f(x)的图象
∴y=f(x)的图象关于x=-2对称
∵函数f(x)在[-4,-2]上是增函数,
∴函数f(x)在[-2,0]上是减函数
∴f(-1)>f(-0.5)>f(0)
∴f(-1)>f(-3.5)>f(0).
故答案为:f(-1)>f(-3.5)>f(0).
又∵由y=f(x-2)向左平移2个单位可得函数y=f(x)的图象
∴y=f(x)的图象关于x=-2对称
∵函数f(x)在[-4,-2]上是增函数,
∴函数f(x)在[-2,0]上是减函数
∴f(-1)>f(-0.5)>f(0)
∴f(-1)>f(-3.5)>f(0).
故答案为:f(-1)>f(-3.5)>f(0).
点评:本题主要考查了偶函数的图象的对称及函数的图象的平移,函数的单调性在大小比较中的应用.

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
函数f(x)=ln(x+
)的图象是( )
| 1 |
| x |
A、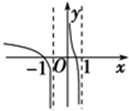 |
B、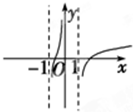 |
C、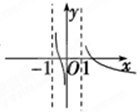 |
D、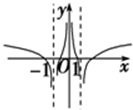 |
用平行于圆锥底面的平面截圆锥,所得截面面积与底面面积的比是1:3,这截面把圆锥母线分成的两段的比是( )
| A、1:3 | ||
B、1:(
| ||
| C、1:9 | ||
D、
|