题目内容
从正六边形六个顶点及其中心这7个点中,任取两个点,则这两个点的距离大于该正六边形边长的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:列举法计算基本事件数及事件发生的概率
专题:计算题,概率与统计
分析:由列举法求出所有可能的情况与不符合条件的情况,从而得到其概率.
解答:
解:从正六边形六个顶点及其中心这7个点中任取两个点共有
=21种情况;
距离等于该正六边形边长有6+6=12种,
故这两个点的距离大于该正六边形边长的概率为
=
.
故选C.
| c | 2 7 |
距离等于该正六边形边长有6+6=12种,
故这两个点的距离大于该正六边形边长的概率为
| 21-12 |
| 21 |
| 3 |
| 7 |
故选C.
点评:本题考查了列举法计算事件数的方法及概率的求法,属于基础题.

练习册系列答案
相关题目
函数f(x)=ln(x+
)的图象是( )
| 1 |
| x |
A、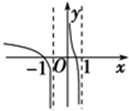 |
B、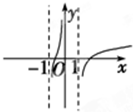 |
C、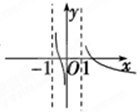 |
D、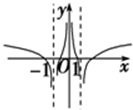 |
设f(x)是定义在R上的奇函数,且f(2)=0,当x>0时,有
>0恒成立,则不等式f(x)>0的解集是( )
| xf′(x)-f(x) |
| x2 |
| A、(-∞,-2)∪(2,+∞) |
| B、(-2,0)∪(0,2) |
| C、(-2,0)∪(2,+∞) |
| D、(-∞,-2)∪(0,2) |
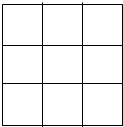 将大小形状相同的4个红球和2个白球放入如图所示的九宫格中,每格至多放一个,要求相邻方格的小球不同色(有公共边的两个方格为相邻),则所有不同的放法种数为( )
将大小形状相同的4个红球和2个白球放入如图所示的九宫格中,每格至多放一个,要求相邻方格的小球不同色(有公共边的两个方格为相邻),则所有不同的放法种数为( )