题目内容
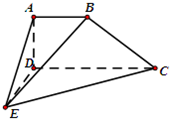 如图,在四棱锥E-ABCD中,AB∥CD,CD=2AB,
如图,在四棱锥E-ABCD中,AB∥CD,CD=2AB,(Ⅰ)在线段CE上找一点M,使得BM∥平面ADE,并给予证明.
(Ⅱ)若平面ADE∩平面BCE=l,试证明:l∥BM.
考点:直线与平面平行的判定,直线与平面平行的性质
专题:空间位置关系与距离
分析:(Ⅰ)找CM的中点,根据面面平行的判定定理证明平面BFM∥平面ADE,即可证明BM∥平面ADE.
(Ⅱ)根据面面平行的性质定理利用平面BFM∥平面ADE即可证明:l∥BM.
(Ⅱ)根据面面平行的性质定理利用平面BFM∥平面ADE即可证明:l∥BM.
解答:
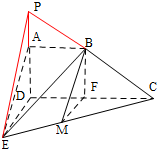 证明:(Ⅰ)取CE的中点M,CD的中点F,连接BF,MF,
证明:(Ⅰ)取CE的中点M,CD的中点F,连接BF,MF,
则BF∥AD,FM∥DE,
∵BF∩FM=F,
∴平面BFM∥平面ADE,
∵BM?平面BFM,
∴BM∥平面ADE.
(Ⅱ)由(Ⅰ)知平面BFM∥平面ADE,
∵平面BFM∩平面BCE=BM,
∴若平面ADE∩平面BCE=l,
则由面面平行的性质可得l∥BM.
 证明:(Ⅰ)取CE的中点M,CD的中点F,连接BF,MF,
证明:(Ⅰ)取CE的中点M,CD的中点F,连接BF,MF,则BF∥AD,FM∥DE,
∵BF∩FM=F,
∴平面BFM∥平面ADE,
∵BM?平面BFM,
∴BM∥平面ADE.
(Ⅱ)由(Ⅰ)知平面BFM∥平面ADE,
∵平面BFM∩平面BCE=BM,
∴若平面ADE∩平面BCE=l,
则由面面平行的性质可得l∥BM.
点评:本题主要考查空间直线和平面平行的判定和性质,根据条件证明平面BFM∥平面ADE是解决本题的关键.

练习册系列答案
相关题目
用更相减损术求30和18的最大公约数时,第三次作的减法为( )
| A、18-16=6 |
| B、12-6=6 |
| C、6-6=0 |
| D、30-18=12 |