题目内容
给出下列命题:
①若
•
=0,则
⊥
;
②|
+
|>|
-
|
③设
,
不共线,
+2
与
+2
能作为一组基底
④若存在一个实数k满足
=k
,则
与
共线
其中正确命题的个数是( ) (第5题)
①若
| a |
| b |
| a |
| b |
②|
| a |
| b |
| a |
| b |
③设
| e1 |
| e2 |
| e1 |
| e2 |
| e2 |
| e1 |
④若存在一个实数k满足
| a |
| b |
| a |
| b |
其中正确命题的个数是( ) (第5题)
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:命题的真假判断与应用
专题:平面向量及应用,简易逻辑
分析:①若非零向量满足
•
=0,则
⊥
,即可判断出;
②|
+
|>|
-
|与|
+
|≤|
-
|都有可能;
③利用向量共线定理与平面向量的基底即可判断出;
④利用向量共线定理即可判断出.
| a |
| b |
| a |
| b |
②|
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
③利用向量共线定理与平面向量的基底即可判断出;
④利用向量共线定理即可判断出.
解答:
解:①若非零向量满足
•
=0,则
⊥
,因此不正确;
②|
+
|>|
-
|与|
+
|≤|
-
|都有可能,因此不正确;
③设
,
不共线,
+2
与
+2
不共线,能作为一组基底,正确;
④若存在一个实数k满足
=k
,则
与
共线,正确.
其中正确命题的个数是2.
故选:B.
| a |
| b |
| a |
| b |
②|
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
③设
| e1 |
| e2 |
| e1 |
| e2 |
| e2 |
| e1 |
④若存在一个实数k满足
| a |
| b |
| a |
| b |
其中正确命题的个数是2.
故选:B.
点评:本题考查了向量共线定理与平面向量的基底、向量垂直与数量积的关系、向量的模,属于基础题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
已知数列{an}的通项公式an=2n,n∈N*,则
+
+
++
=( )
|
|
|
|
| A、-16096 |
| B、-16104 |
| C、-16112 |
| D、-16120 |
用更相减损术求30和18的最大公约数时,第三次作的减法为( )
| A、18-16=6 |
| B、12-6=6 |
| C、6-6=0 |
| D、30-18=12 |
在正方体ABCD-A1B1C1D1中向量表达式
-
+
化简后的结果是( )
| DD1 |
| AB |
| BC |
A、
| ||
B、
| ||
C、
| ||
D、
|
定义:如果函数f(x)在[a,b]上存在x1,x2(a<x1<x2<b),满足f′(x1)=
,f′(x2)=
,则称函数f(x)是[a,b]上的“双中值函数”.已知函数f(x)=
x3-x2+a是[0,a]上“双中值函数”,则实数a的取值范围是( )
| f(b)-f(a) |
| b-a |
| f(b)-f(a) |
| b-a |
| 1 |
| 3 |
| A、(1,3) | ||||
B、(
| ||||
C、(1,
| ||||
D、(1,
|
 执行右边的程序框图,若第一次输入的a的值为-1.2,第二次输入的a的值为1.2,则第一次、第二次输出的a的值分别为
执行右边的程序框图,若第一次输入的a的值为-1.2,第二次输入的a的值为1.2,则第一次、第二次输出的a的值分别为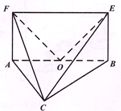 如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,AC=BC,O为AB的中点,OF⊥EC.
如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,AC=BC,O为AB的中点,OF⊥EC.