题目内容
15．已知x，y满足$\left\{\begin{array}{l}x+y-2≥0\\ x+2y-4≤0\\ x-3≤0\end{array}\right.$，则3x-2y的最大值为（ ）| A． | -4 | B． | 8 | C． | 11 | D． | 13 |
分析 首先画出可行域，利用目标函数的几何意义求最大值．
解答 解：由已知得到可行域如图：
设z=3x-2y，得到y=$\frac{3}{2}x-\frac{z}{2}$，
当此直线经过图中A（3，-1）时
在y轴的截距最小，z最大，
所以z 的最大值为3×3+2=11；
故选C．
点评 本题考查了简单线性规划问题；首先正确画出可行域，然后利用目标函数的几何意义求最值；利用了数形结合的思想．
练习册系列答案
名校联盟快乐课堂系列答案
相关题目
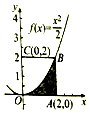如图，利用随机模拟的方法可以估计图中由曲线$y=\frac{x^2}{2}$与两直线x=2及y=0所围成的阴影部分的面积S：
3．已知全集U=Z，A={x|x2-x-2＜0，x∈Z}，B={-1，0，1，2}，则（∁UA）∩B等于（ ）
| A． | {-1，2} | B． | {-1，0} | C． | {0，1} | D． | {1，2} |
（1）在Rt ABC 中，CA CB，斜边AB 上的高为 h，则$\frac{1}{{h}^{2}}$ $\frac{1}{C{A}^{2}}$ $\frac{1}{C{B}^{2}}$，类比此性质，如图，在四面体 PABC中，若 PA，PB，PC两两垂直，底面ABC上的高为 h，可猜想得到的结论为$\frac{1}{{h}^{2}}$=$\frac{1}{P{A}^{2}}$+$\frac{1}{P{B}^{2}}$+$\frac{1}{P{C}^{2}}$．