题目内容
10.下列说法中不正确的个数是( )①对于定义域内的可导函数f(x),f(x)在某处的导数为0是f(x)在该处取到极值的必要不充分条件;
②命题“?x∈R,cosx≤1”的否定是“?x0∈R,cosx0≥1”;
③若一个命题的逆命题为真,则它的否命题一定为假.
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 对于①,可通过举f(x)=x3,可得f(x)在x=0处的导数为0,但f(x)在R上递增,无极值.结合极值和充分必要条件的定义即可判断;
对于②,运用全称命题的否定为特称命题,注意量词的变化和不等号的变化,即可判断;
对于③,运用逆命题与否命题等价,即可判断.
解答 解:对于①,对于定义域内的可导函数f(x),f(x)在某处的导数为0,
比如f(x)=x3,f′(x)=3x2≥0,由f(x)在x=0处的导数为0,但f(x)在R上递增,无极值;
反之,若f(x)在某点处取到极值,则由极值的定义可得f(x)在某处的导数为0,
故f(x)在某处的导数为0是f(x)在该处取到极值的必要不充分条件,则①正确;
对于②,命题“?x∈R,cosx≤1”的否定是“?x0∈R,cosx0>1”,则②错误;
对于③,若一个命题的逆命题为真,由互为逆否命题等价,则它的否命题一定为真,则③错误.
其中不正确的个数为2.
故选:C.
点评 本题考查命题的真假判断和应用,主要是充分必要条件的判断和命题的否定,以及四种命题和等价命题的判断,考查导数的运用:求极值,考查判断能力,属于基础题和易错题.

练习册系列答案
相关题目
15.已知x,y满足$\left\{\begin{array}{l}x+y-2≥0\\ x+2y-4≤0\\ x-3≤0\end{array}\right.$,则3x-2y的最大值为( )
| A. | -4 | B. | 8 | C. | 11 | D. | 13 |
2.已知集合A={x|x2-2x-3≤0},B={x|4x≥2},则A∪B=( )
| A. | $[{\frac{1}{2},3}]$ | B. | $[{\frac{1}{2},3})$ | C. | (-∞,3] | D. | [-1,+∞) |
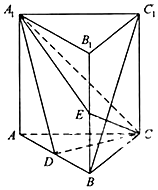 如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=$\frac{{\sqrt{2}}}{2}$AB.
如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=$\frac{{\sqrt{2}}}{2}$AB.