题目内容
20.△ABC中,角A、B、C所对边分别为a、b、c,cosA=$\frac{5}{13}$,tan$\frac{B}{2}+cot\frac{B}{2}=\frac{10}{3}$,c=21;(1)求sinC的值;
(2)求△ABC的面积.
分析 (1)先根据弦切之间的关系对tan$\frac{B}{2}+cot\frac{B}{2}=\frac{10}{3}$进行化简,再由二倍角公式可得到sinB的值,结合cosA的值可判断B为锐角,进而由sinC=sin(A+B)根据两角和与差的正弦公式和(1)中的sinB,sinA,cosB,cosA的值可求得sinC的值.
(2)再由正弦定理可求得a的值,最后根据三角形的面积公式可求得答案.
解答 解:(1)由tan$\frac{B}{2}+cot\frac{B}{2}=\frac{10}{3}$=$\frac{si{n}^{2}\frac{B}{2}+co{s}^{2}\frac{B}{2}}{sin\frac{B}{2}cos\frac{B}{2}}$=$\frac{1}{sin\frac{B}{2}cos\frac{B}{2}}$,
得sinB=$\frac{3}{5}$,
∵cosA=$\frac{5}{13}$,∴sinA=$\frac{12}{13}$>sinB,∴B为锐角,可得cosB=$\frac{4}{5}$,
∴sinC=sin(A+B)=sinAcosB+cosAsinB=$\frac{12}{13}$×$\frac{4}{5}$+$\frac{5}{13}$×$\frac{3}{5}$=$\frac{63}{65}$.
(2)∵c=21,
∴a=$\frac{csinA}{sinC}$=$\frac{21×\frac{12}{13}}{\frac{63}{65}}$=20,
∴S△ABC=$\frac{1}{2}$acsinB=$\frac{1}{2}$×20×21×$\frac{3}{5}$=126.
点评 本题主要考查同角三角函数的基本关系、二倍角公式、两角和与差的公式、正弦定理的应用,三角函数内的公式比较多,容易记混,在平时一定要多注意积累,到考试时才能做到游刃有余,属于基础题.

| A. | -4 | B. | 8 | C. | 11 | D. | 13 |
| x | 1 | 2 | 3 | 4 |
| y | 0.5 | 1 | 1.5 | 3 |
参考公式:
用最小二乘法求线性回归方程系数公式:$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}},\hat a=\overline y-\hat b\overline x$.
| A. | 2n-1 | B. | 2n-1 | C. | 2×3n-1. | D. | $\frac{1}{2}({{3^n}-1})$ |
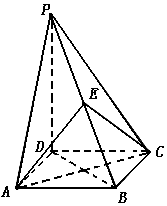 如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.