题目内容
7.已知函数f(x)=p+qsin3x的最大值与最小值分别为3和-1,求函数g(x)=(p-q)cos3x的最大值与最小值.分析 由已知中函数f(x)=p+qsin3x的最大值与最小值分别为3和-1,求出p,q值,进而可得函数g(x)=(p-q)cos3x的最大值与最小值.
解答 解:∵函数f(x)=p+qsin3x的最大值与最小值分别为3和-1,
∴p=1,q=2,或p=1,q=-2,
①当p=1,q=2时,g(x)=(p-q)cos3x=-cos3x的最大值为1,最小值为-1;
②当p=1,q=-2时,g(x)=(p-q)cos3x=3cos3x的最大值为3,最小值为-3;
点评 本题考查的知识点是函数的最值及其几何意义,三角函数的图象和性质,难度中档.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
17.设α,β是两个不同的平面,直线l满足l?β,以下命题中错误的命题是( )
| A. | 若l∥α,α⊥β,则l⊥β | B. | 若l∥α,α∥β,则l∥β | C. | 若l⊥α,α∥β,则l⊥β | D. | 若l⊥α,α⊥β,则l∥β |
15.已知x,y满足$\left\{\begin{array}{l}x+y-2≥0\\ x+2y-4≤0\\ x-3≤0\end{array}\right.$,则3x-2y的最大值为( )
| A. | -4 | B. | 8 | C. | 11 | D. | 13 |
2.已知集合A={x|x2-2x-3≤0},B={x|4x≥2},则A∪B=( )
| A. | $[{\frac{1}{2},3}]$ | B. | $[{\frac{1}{2},3})$ | C. | (-∞,3] | D. | [-1,+∞) |
12.已知数列{an}的前n项和为Sn,a1=1,2Sn=an+1,则an+1=( )
| A. | 2n-1 | B. | 2n-1 | C. | 2×3n-1. | D. | $\frac{1}{2}({{3^n}-1})$ |
16.设函数$f(x)=sin(x+\frac{7π}{4})+cos(x-\frac{3π}{4})$则( )
| A. | y=f(x)的最小正周期是π,其图象关于$x=-\frac{π}{4}$对称 | |
| B. | y=f(x)的最小正周期是2π,其图象关于$x=\frac{π}{2}$对称 | |
| C. | y=f(x)的最小正周期是π,其图象关于$x=\frac{π}{2}$对称 | |
| D. | y=f(x)的最小正周期是2π,其图象关于$x=-\frac{π}{4}$对称 |
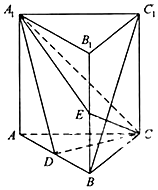 如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=$\frac{{\sqrt{2}}}{2}$AB.
如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=$\frac{{\sqrt{2}}}{2}$AB.