题目内容
设平面α∩平面β=l,点A,B∈α,点C∈β,且A,B,C均不在直线l上,给出四个命题:
①
⇒α⊥β;②
⇒α⊥平面ABC;③
⇒l⊥平面ABC;④AB∥l⇒l∥平面ABC.
其中正确的命题是( )
①
|
|
|
其中正确的命题是( )
| A、①与② | B、②与③ |
| C、①与③ | D、②与④ |
考点:直线与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:根据空间中的直线,平面之间的平行,垂直的判定,性质定理判断分析,可以得出答案.
解答:
解:①不正确,∵l⊥AB,l⊥AC时,平面α与平面β的夹角不一定为90°;
②正确,∵l⊥AC,l⊥BC,AC∩BC=C,∴α⊥平面ABC;
③不正确,∵AB∥l时,明显不会l⊥平面ABC;
④正确,∵AB∥l,且A,B,C均不在直线l上,故l∥平面ABC.
故选:D.

②正确,∵l⊥AC,l⊥BC,AC∩BC=C,∴α⊥平面ABC;
③不正确,∵AB∥l时,明显不会l⊥平面ABC;
④正确,∵AB∥l,且A,B,C均不在直线l上,故l∥平面ABC.
故选:D.

点评:本题主要考察了直线与平面垂直的判定,直线与平面平行的判定,属于基本知识的考查.

练习册系列答案
相关题目
如图所示是一个四棱锥的三视图,则该几何体的体积为( )
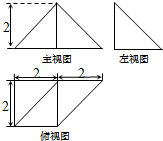

| A、4 | ||||
B、
| ||||
| C、12 | ||||
D、
|
已知函数f(x)=sin(
x+θ)-
cos(
x+θ)(|θ|<
)的图象关于y中对称,则y=f(x)在下列哪个区间上是减函数( )
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| π |
| 2 |
A、(0,
| ||||
B、(
| ||||
C、(-
| ||||
D、(
|
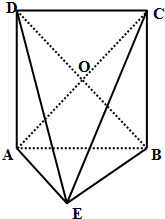 如图,在横放得四棱锥E-ABCD中,底面ABCD是正方形,∠DAE=90°,且△ABE是等腰直角三角形,其中∠BAE=90°,连接AC、BD交于点O.
如图,在横放得四棱锥E-ABCD中,底面ABCD是正方形,∠DAE=90°,且△ABE是等腰直角三角形,其中∠BAE=90°,连接AC、BD交于点O. 如图,海上有A,B两个小岛相距10km,船O将保持观望A岛和B岛所成的视角为60°,现从船O上派下一只小艇沿BO方向驶至C处进行作业,且OC=BO.设AC=xkm.
如图,海上有A,B两个小岛相距10km,船O将保持观望A岛和B岛所成的视角为60°,现从船O上派下一只小艇沿BO方向驶至C处进行作业,且OC=BO.设AC=xkm.