题目内容
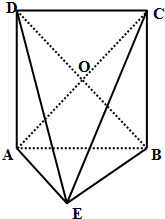如图，在横放得四棱锥E-ABCD中，底面ABCD是正方形，∠DAE=90°，且△ABE是等腰直角三角形，其中∠BAE=90°，连接AC、BD交于点O．（1）求证：BD⊥平面AEC；
（2）若二面角A-BD-E的大小为60°，且直线EC与平面ABCD所成的角为θ，求sinθ．
考点：二面角的平面角及求法,直线与平面垂直的判定
专题：计算题,空间位置关系与距离
分析：（1）由已知，DA⊥AE，BA⊥AE，得到AE⊥平面ABCD，可得AE⊥BD，又AC⊥BC，从而有BD⊥平面AEC；
（2）连接EO，由（1）知BD⊥AO，BD⊥EO，∠AOE为二面角A-BD-E的平面角，即∠AOE=60°，不妨设AE=
，则可求得EC=
，从而可求sinθ的值．
（2）连接EO，由（1）知BD⊥AO，BD⊥EO，∠AOE为二面角A-BD-E的平面角，即∠AOE=60°，不妨设AE=
| 3 |
| 7 |
解答：
解：（1）由已知，DA⊥AE，BA⊥AE，得到AE⊥平面ABCD，故AE⊥BD，又AC⊥BC，故BD⊥平面AEC；-----------5分
（2）连接EO，由（1）知BD⊥AO，BD⊥EO，∠AOE为二面角A-BD-E的平面角，即∠AOE=60°．------------7分
不妨设AE=
，则在Rt△AOE中，AO=1，AC=2，
又由（1）知AE⊥平面ABCD，∠ACE为直线EC在平面ABCD所成的角，即∠ACE=θ．在Tt△ACE中，EC=
=
，
故sinθ=
=
．----------------12分
（2）连接EO，由（1）知BD⊥AO，BD⊥EO，∠AOE为二面角A-BD-E的平面角，即∠AOE=60°．------------7分
不妨设AE=
| 3 |
又由（1）知AE⊥平面ABCD，∠ACE为直线EC在平面ABCD所成的角，即∠ACE=θ．在Tt△ACE中，EC=
| AE2+AC2 |
| 7 |
故sinθ=
| AE |
| EC |
| ||
| 7 |
点评：本题主要考察了二面角的平面角及求法，直线与平面垂直的判定，属于基本知识的考查．
练习册系列答案
通城学典默写能手系列答案
相关题目
设平面α∩平面β=l，点A，B∈α，点C∈β，且A，B，C均不在直线l上，给出四个命题：
①
⇒α⊥β；②
⇒α⊥平面ABC；③
⇒l⊥平面ABC；④AB∥l⇒l∥平面ABC．
其中正确的命题是（ ）
①
|
|
|
其中正确的命题是（ ）
| A、①与② | B、②与③ |
| C、①与③ | D、②与④ |
已知H是球O的直径AB上的一点，AH：HB=1：2，AH⊥平面α，H为垂足，α截球O所得截面的面积为π，则球O的表面积为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|