题目内容
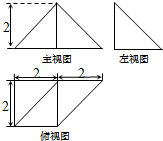
如图所示是一个四棱锥的三视图，则该几何体的体积为（ ）
| A、4 | ||||
B、
| ||||
| C、12 | ||||
D、
|
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：根据几何体的三视图，得出该几何体是底面为直角梯形，高为2的四棱锥．
解答：
解：根据几何体的三视图，得出该几何体是底面为直角梯形，高为2的四棱锥，
该四棱锥的体积为
V四棱锥=
S梯形h
=
×
×（2+4）×2×2
=4．
故选：A．
该四棱锥的体积为
V四棱锥=
| 1 |
| 3 |
=
| 1 |
| 3 |
| 1 |
| 2 |
=4．
故选：A．
点评：本题考查了空间几何体三视图的应用问题，解题时应根据三视图，得出几何体是什么图形，是基础题．
练习册系列答案
相关题目
设平面α∩平面β=l，点A，B∈α，点C∈β，且A，B，C均不在直线l上，给出四个命题：
①
⇒α⊥β；②
⇒α⊥平面ABC；③
⇒l⊥平面ABC；④AB∥l⇒l∥平面ABC．
其中正确的命题是（ ）
①
|
|
|
其中正确的命题是（ ）
| A、①与② | B、②与③ |
| C、①与③ | D、②与④ |
将函数y=sin2x的图象向左平移
个单位，再向上平移1个单位，所得图象的函数解析式是（ ）
| π |
| 4 |
| A、y=cos2x | ||
B、y=1+sin(2x+
| ||
| C、y=2cos2x | ||
| D、y=2sin2x |