题目内容
已知数列{an}中,a1=1,an+1=
(n∈N*).
(1)求证:{
+
}是等比数列;
(2)数列{bn}满足bn=(3n-1)•
•an,数列{bn}的前n项和为Tn,若不等式(-
)nλ<Tn+
对一切n∈N*恒成立,求λ的取值范围.
| an |
| an+3 |
(1)求证:{
| 1 |
| an |
| 1 |
| 2 |
(2)数列{bn}满足bn=(3n-1)•
| n |
| 2n |
| 1 |
| 2 |
| n |
| 2n-1 |
考点:数列与不等式的综合,等比数列的性质
专题:等差数列与等比数列
分析:(1)由a1=1,an+1=
(n∈N*)知,
+
=3(
+
),由此能证明{
+
}是以
为首项,3为公比的等比数列.
(2)由
+
=
×3n-1=
,得an=
,bn=
,由此利用错位相减法求出Tn=4-
,从而(-
)nλ<4-
,由此能求出λ的取值范围.
| an |
| an+3 |
| 1 |
| an+1 |
| 1 |
| 2 |
| 1 |
| an |
| 1 |
| 2 |
| 1 |
| an |
| 1 |
| 2 |
| 3 |
| 2 |
(2)由
| 1 |
| an |
| 1 |
| 2 |
| 3 |
| 2 |
| 3n |
| 2 |
| 2 |
| 3n-1 |
| n |
| 2n-1 |
| n+2 |
| 2n-1 |
| 1 |
| 2 |
| 1 |
| 2n-2 |
解答:
(1)证明:由a1=1,an+1=
(n∈N*)知,
+
=3(
+
),
又
+
=
,
∴{
+
}是以
为首项,3为公比的等比数列.…(5分)
(2)解:由(1)知
+
=
×3n-1=
,
∴an=
,∴bn=
…(6分)
Tn=1×
+2×
+3×
+…+(n-1)×
+n×
,
=1×
+2×
+…+(n-1)×
+n×
,…(7分)
两式相减得
=
+
+
+…+
-n×
=2-
,
∴Tn=4-
…(10分)
∴(-
)nλ<4-
若n为偶数,则(
)nλ<4-
,即λ<2n+2-4,解得λ<12
若n为奇数,则-(
)nλ<4-
-λ<2n+2-4,解得-λ<4,
∴λ>-4∴-4<λ<12.…(14分)
| an |
| an+3 |
| 1 |
| an+1 |
| 1 |
| 2 |
| 1 |
| an |
| 1 |
| 2 |
又
| 1 |
| a1 |
| 1 |
| 2 |
| 3 |
| 2 |
∴{
| 1 |
| an |
| 1 |
| 2 |
| 3 |
| 2 |
(2)解:由(1)知
| 1 |
| an |
| 1 |
| 2 |
| 3 |
| 2 |
| 3n |
| 2 |
∴an=
| 2 |
| 3n-1 |
| n |
| 2n-1 |
Tn=1×
| 1 |
| 20 |
| 1 |
| 21 |
| 1 |
| 22 |
| 1 |
| 2n-2 |
| 1 |
| 2n-1 |
| Tn |
| 2 |
| 1 |
| 21 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
| 1 |
| 2n |
两式相减得
| Tn |
| 2 |
| 1 |
| 20 |
| 1 |
| 21 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
| 1 |
| 2n |
| n+2 |
| 2n |
∴Tn=4-
| n+2 |
| 2n-1 |
∴(-
| 1 |
| 2 |
| 1 |
| 2n-2 |
若n为偶数,则(
| 1 |
| 2 |
| 1 |
| 2n-2 |
若n为奇数,则-(
| 1 |
| 2 |
| 1 |
| 2n-2 |
∴λ>-4∴-4<λ<12.…(14分)
点评:本题考查等比数列的证明,考查实数的取值范围的求法,解题时要认真审题,注意构造法的合理运用.

练习册系列答案
相关题目
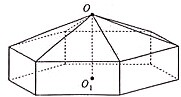 请您设计一个帐篷,它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如图所示).试问当帐篷的顶点O到底面中心O1的距离为多少时,帐篷的体积为16
请您设计一个帐篷,它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如图所示).试问当帐篷的顶点O到底面中心O1的距离为多少时,帐篷的体积为16