题目内容
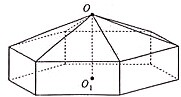请您设计一个帐篷，它下部的形状是高为1m的正六棱柱，上部的形状是侧棱长为3m的正六棱锥（如图所示）．试问当帐篷的顶点O到底面中心O1的距离为多少时，帐篷的体积为16| 3 |
考点：点、线、面间的距离计算,组合几何体的面积、体积问题
专题：空间位置关系与距离
分析：设OO1为xm，则1＜x＜4，设题设可得正六棱锥底面边长为
=
，从而帐篷的体积为V（x）=
(8+2x-x2)[
(x-1)+1]=
(16+12x-x3)，由此利用导数性质能求出当OO1为2m时，帐逢的体积最大，为16
m3．
| 32-(x-1)2 |
| 8+2x-x2 |
2
| ||
| 2 |
| 1 |
| 3 |
| ||
| 2 |
| 3 |
解答：
解：设OO1为xm，则1＜x＜4，
设题设可得正六棱锥底面边长为（单位：m）
=
，
于是底面正六边形的面积为（单位：m2）
6•
•(
)2=
(8+2x-x2)，
帐篷的体积为（单位：m3）
V（x）=
(8+2x-x2)[
(x-1)+1]=
(16+12x-x3)，
求导数，得V′(x)=
(12-3x2)，
令V′（x）=0，解得x=-2（不合题意，舍去），x=2
当1＜x＜2时，V′（x）＞0，V（x）为增函数，
当2＜x＜4时，V′（x）＜0，V（x）为减函数
所以当x=2时，V（x）最大，
此时V（x）=
(16+12x-x3)=16
．
故当OO1为2m时，帐逢的体积最大，为16
m3．
设题设可得正六棱锥底面边长为（单位：m）
| 32-(x-1)2 |
| 8+2x-x2 |
于是底面正六边形的面积为（单位：m2）
6•
| ||
| 4 |
| 8+2x-x2 |
2
| ||
| 2 |
帐篷的体积为（单位：m3）
V（x）=
2
| ||
| 2 |
| 1 |
| 3 |
| ||
| 2 |
求导数，得V′(x)=
| ||
| 2 |
令V′（x）=0，解得x=-2（不合题意，舍去），x=2
当1＜x＜2时，V′（x）＞0，V（x）为增函数，
当2＜x＜4时，V′（x）＜0，V（x）为减函数
所以当x=2时，V（x）最大，
此时V（x）=
| ||
| 2 |
| 3 |
故当OO1为2m时，帐逢的体积最大，为16
| 3 |
点评：本题考查当帐篷的顶点O到底面中心O1的距离为多少时，帐篷的体积为16
的求法，是中档题，解题时要注意几何体体积的求法和导数性质的合理运用．
| 3 |
练习册系列答案
相关题目
已知集合M={（x，y）|y=x2}，N={y|x2+y2=2}，则M∩N=（ ）
| A、{（1，1），（-1，1）} | ||
| B、∅ | ||
| C、[0，1] | ||
D、[0，
|
若集合M={x|y=
}，N={x|y=log2（1-x）}，则集合M∩N=（ ）
| 1 | ||
|
| A、（-∞，1） | B、（1，+∞） |
| C、（0，1） | D、R |
下列说法中正确的是（ ）
| A、三点确定一个平面 |
| B、两条直线确定一个平面 |
| C、两两相交的三条直线一定在同一平面内 |
| D、过同一点的三条直线不一定在同一平面内 |