题目内容
6.设正三棱锥A-BCD(底面是正三角形,顶点在底面的射影为底面中心)的所有顶点都在球O的球面上,BC=2,E,F分别是AB,BC的中点,EF⊥DE,则球O的表面积为( )| A. | $\frac{3π}{2}$ | B. | 6π | C. | 8π | D. | 12π |
分析 根据EF与DE的垂直关系,结合正棱锥的性质,判断三条侧棱互相垂直,再求得侧棱长,根据表面积公式计算即可
解答 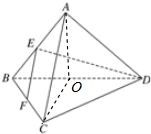 解:∵E、F分别是AB、BC的中点,∴EF∥AC,
解:∵E、F分别是AB、BC的中点,∴EF∥AC,
又∵EF⊥DE,
∴AC⊥DE,
取BD的中点O,连接AO、CO,
∵三棱锥A-BCD为正三棱锥,
∴AO⊥BD,CO⊥BD,∴BD⊥平面AOC,又AC?平面AOC,∴AC⊥BD,
又DE∩BD=D,∴AC⊥平面ABD;
∴AC⊥AB,
设AC=AB=AD=x,则x2+x2=4⇒x=$\sqrt{2}$,
所以三棱锥对应的长方体的对角线为$\sqrt{3×2}$=$\sqrt{6}$,
所以它的外接球半径为$\frac{\sqrt{6}}{2}$,
∴球O的表面积为$4π•\frac{6}{4}$=6π
故选:B.
点评 本题考查了正三棱锥的外接球表面积求法,关键是求出三棱锥的三条侧棱长度,得到对应的长方体对角线,即外接球的直径.

练习册系列答案
相关题目
16. 如图,阴影部分的面积为( )
如图,阴影部分的面积为( )
 如图,阴影部分的面积为( )
如图,阴影部分的面积为( )| A. | 9 | B. | $\frac{9}{2}$ | C. | $\frac{13}{6}$ | D. | $\frac{7}{3}$ |
17.已知全集U={x|x≤9,x∈N+},集合A={1,2,3},B={3,4,5,6},则∁U(A∪B)=( )
| A. | {3} | B. | {7,8} | C. | {7,8,9} | D. | {1,2,3,4,5,6} |
1.f(x)为奇函数,当x>0时,f(x)=π-arccos(sinx)则x<0时,f(x)=( )
| A. | arccos(sinx) | B. | π+arccos(sinx) | C. | -arccos(sinx) | D. | -π-arccos(sinx) |
11.已知圆锥底面半径为2,高为$\sqrt{5}$,有一球在该圆锥内部且与它的侧面和底面都相切,则这个球的体积为( )
| A. | $\frac{{32\sqrt{5}π}}{25}$ | B. | $\frac{{32\sqrt{5}π}}{75}$ | C. | $\frac{8π}{5}$ | D. | $\frac{16π}{5}$ |
18.曲线y=x2-1与直线y=2x+2轴围成的封闭部分的面积为( )
| A. | $\frac{17}{3}$ | B. | $\frac{22}{3}$ | C. | $\frac{32}{3}$ | D. | $\frac{35}{3}$ |