题目内容
11．已知圆锥底面半径为2，高为$\sqrt{5}$，有一球在该圆锥内部且与它的侧面和底面都相切，则这个球的体积为（ ）| A． | $\frac{{32\sqrt{5}π}}{25}$ | B． | $\frac{{32\sqrt{5}π}}{75}$ | C． | $\frac{8π}{5}$ | D． | $\frac{16π}{5}$ |
分析 画出轴截面图形，设出球的半径，求出圆锥的高，利用三角形相似，求出球的半径．
解答 
解：几何体的轴截面如图，设球的半径为r，球与圆锥侧面相切，则OE垂直于AB于E，BD垂直AD，E为AB上一点，O为AD上一点，
则△AEO～△ADB，∴$\frac{r}{2}=\frac{\sqrt{5}-r}{3}$，
∴r=$\frac{2\sqrt{5}}{5}$，
∴球的体积为$\frac{4}{3}π•（\frac{2\sqrt{5}}{5}）^{3}$=$\frac{32\sqrt{5}}{75}π$
故选：B．
点评 本题考查球的外接体问题，考查计算能力，是基础题．
练习册系列答案
相关题目
19．已知数列{an}的通项公式为${a_n}={（{\frac{3}{4}}）^{n-1}}[{{{（{\frac{3}{4}}）}^{n-1}}-1}]$，则关于an的最大项、最小项叙述正确的是（ ）
| A． | 最大项为a1、最小项为a3 | B． | 最大项为a1、最小项不存在 | ||
| C． | 最大项不存在、最小项为a3 | D． | 最大项为a1、最小项为a4 |
6．设正三棱锥A-BCD（底面是正三角形，顶点在底面的射影为底面中心）的所有顶点都在球O的球面上，BC=2，E，F分别是AB，BC的中点，EF⊥DE，则球O的表面积为（ ）
| A． | $\frac{3π}{2}$ | B． | 6π | C． | 8π | D． | 12π |
20．
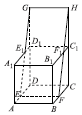如图所示，在棱长为a的正方体ABCD-A1B2C3D4中，点E，F分别在棱AD，BC上，且AE=BF=$\frac{1}{3}$a．过EF的平面绕EF旋转，与DD1、CC1的延长线分别交于G，H点，与A1D1、B1C1分别交于E1，F1点．当异面直线FF1与DD1所成的角的正切值为$\frac{1}{3}$时，|GF1|=（ ）
如图所示，在棱长为a的正方体ABCD-A1B2C3D4中，点E，F分别在棱AD，BC上，且AE=BF=$\frac{1}{3}$a．过EF的平面绕EF旋转，与DD1、CC1的延长线分别交于G，H点，与A1D1、B1C1分别交于E1，F1点．当异面直线FF1与DD1所成的角的正切值为$\frac{1}{3}$时，|GF1|=（ ）| A． | $\frac{\sqrt{19}a}{3}$ | B． | $\frac{\sqrt{19}a}{9}$ | C． | $\frac{\sqrt{2}a}{3}$ | D． | $\frac{\sqrt{2}a}{9}$ |
