题目内容
已知f（x-2）=ax2+4x+a-2（a为负整数），若存在实数m使得f（m-2）=0，求函数f（x）的解析式．
考点：二次函数的性质
专题：函数的性质及应用
分析：由题意知函数在x轴上有零点，所以ax2+4x+a-2=0有实数根，由判别式△≥0，求出a的值，将a代入函数整理即可．
解答：
解：令ax2+4x+a-2=0，
由题意得：16-4a（a-2）≥0，
解得：1-
≤a≤1+
，
又a为负整数，
∴a=-1，
∴f（x-2）=-x2+4x-3=-（x-2）2+1，
∴f（x）=-x2+1．
由题意得：16-4a（a-2）≥0，
解得：1-
| 5 |
| 5 |
又a为负整数，
∴a=-1，
∴f（x-2）=-x2+4x-3=-（x-2）2+1，
∴f（x）=-x2+1．
点评：本题考察了二次函数的性质，函数的零点问题，是一道中档题．
练习册系列答案
相关题目
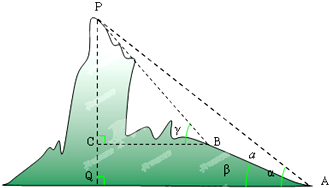如图，在山脚A测得出山顶P的仰角为α，沿倾斜角为β的斜坡向上走a米到B，在B处测得山顶P的仰角为γ，求证：山高h=