题目内容

求函数y=
2+log
1
2
x
+
tanx
的定义域．
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：根据函数成立的条件，建立不等式组即可得到结论．
解答： 解：要使函数有意义，则
2+log
1
2
x≥0
tanx≥0
⇒
0＜x≤4
kπ≤x＜kπ+
π
2
，
得0＜x＜
π
2
，或π≤x≤4，
即函数的定义域为（0，
π
2
）∪[π，4]．
点评：本题主要考查函数定义域的求法，要求熟练掌握常见函数成立的条件．
练习册系列答案
相关题目
已知函数f（x）=
x+5
x+2
．
（1）若x∈[1，10]，求f（x）的取值范围；
（2）证明函数f（x）的图象关于（-2，1）对称．
求函数y=2sin（2x+
π
3
）最小正周期，单调递增区间，对称轴，对称中心．
已知函数f（x）=
3
sinxcosx-cos2x-
1
2
，（x∈R）．
（1）求函数f（x）的最小正周期；
（2）求f（x）单调增区间．
（3）若x∈[
π
4
，
π
2
]，求f（x）的最值．
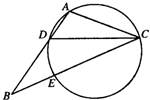如图，在△ABC中，CD是∠ACB的角平分线，△ADC的外接圆交BC于点E，AB=2AC
（Ⅰ）求证：BE=2AD；
（Ⅱ）当AC=3，EC=6时，求AD的长．
已知f（x-2）=ax2+4x+a-2（a为负整数），若存在实数m使得f（m-2）=0，求函数f（x）的解析式．
已知函数f（x）=a|x|+
2
ax
（a＞0，a≠1）
（1）若a＞1，且关于x的方程f（x）=m有两个不同的正数解，求实数m的取值范围；
（2）设函数g（x）=f（-x），x∈[-2，+∞），满足如下性质：若存在最大（小）值，则最大（小）值与a无关．试求a的取值范围．
已知向量
m
=（cosx，-sinx），
n
=（cosx，sinx-2
3
cosx），x∈R，令f（x）=
m
•
n
，
（1）求函数f（x）的单调递增区间；
（2）当x∈[0，
π
4
]时，求函数f（x）的值域．
函数f（x）=tan2（x+
π
4
）的单调递增区间为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网