题目内容
“m=1”是“函数f(x)=x2-6mx+6在区间(-∞,3]上为减函数”的( )
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据二次函数的图象和性质,求出函数f(x)=x2-6mx+6在区间(-∞,3]上为减函数的m的取值,进而根据充要条件的定义,得到答案.
解答:
解:若函数f(x)=x2-6mx+6在区间(-∞,3]上为减函数,则3m≥3,
解得:m≥1,
故“m=1”是“函数f(x)=x2-6mx+6在区间(-∞,3]上为减函数”的充分不必要条件,
故选:B
解得:m≥1,
故“m=1”是“函数f(x)=x2-6mx+6在区间(-∞,3]上为减函数”的充分不必要条件,
故选:B
点评:判断充要条件的方法是:
①若p⇒q为真命题且q⇒p为假命题,则命题p是命题q的充分不必要条件;
②若p⇒q为假命题且q⇒p为真命题,则命题p是命题q的必要不充分条件;
③若p⇒q为真命题且q⇒p为真命题,则命题p是命题q的充要条件;
④若p⇒q为假命题且q⇒p为假命题,则命题p是命题q的即不充分也不必要条件.
⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.
①若p⇒q为真命题且q⇒p为假命题,则命题p是命题q的充分不必要条件;
②若p⇒q为假命题且q⇒p为真命题,则命题p是命题q的必要不充分条件;
③若p⇒q为真命题且q⇒p为真命题,则命题p是命题q的充要条件;
④若p⇒q为假命题且q⇒p为假命题,则命题p是命题q的即不充分也不必要条件.
⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
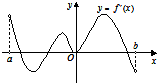 函数f(x)的定义域为开区间(a,b),导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在开区间(a,b)内有极小值( )
函数f(x)的定义域为开区间(a,b),导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在开区间(a,b)内有极小值( )| A、2个 | B、1个 | C、3个 | D、4个 |
设函数f(x)=(x-1)2+n (x∈[-1,3],n∈N*)的最小值为an,最大值为bn,记cn=bn2-anbn,则{cn}是( )
| A、常数数列 |
| B、公比不为1的等比数列 |
| C、公差不为0的等差数列 |
| D、非等差数列也非等比数列 |
将4个不同颜色的小球全部放入不同标号的3个盒子中,可以有一个或者多个盒子空着的放法种数为( )
| A、96 | B、36 | C、64 | D、81 |
设
为复数z的共轭复数,且
•i=1+2i,则z等于( )
. |
| z |
. |
| z |
| A、2-i | B、2+i |
| C、1+2i | D、1-2i |
设x,y∈R,向量
=(x,1),
=(1,y),
=(2,-4)且
⊥
,
∥
,则x+y=( )
| a |
| b |
| c |
| a |
| c |
| b |
| c |
| A、0 | B、-4 | C、2 | D、4 |
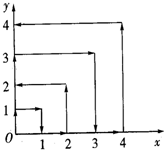 如图,一个质点从原点出发,在与y轴.x轴平行的方向按(0,0)→(0,1)→(1,1)→(1,0)→(2,0)→(2,2)…的规律向前移动,且每秒钟移动一个单位长度,那么到第2011秒时,这个质点所处位置的坐标是( )
如图,一个质点从原点出发,在与y轴.x轴平行的方向按(0,0)→(0,1)→(1,1)→(1,0)→(2,0)→(2,2)…的规律向前移动,且每秒钟移动一个单位长度,那么到第2011秒时,这个质点所处位置的坐标是( )| A、(13,44) |
| B、(14,44) |
| C、(44,13) |
| D、(44,14) |