题目内容
设函数f(x)=(x-1)2+n (x∈[-1,3],n∈N*)的最小值为an,最大值为bn,记cn=bn2-anbn,则{cn}是( )
| A、常数数列 |
| B、公比不为1的等比数列 |
| C、公差不为0的等差数列 |
| D、非等差数列也非等比数列 |
考点:等差关系的确定,数列的函数特性
专题:等差数列与等比数列
分析:依题意,可得an=n,bn=n+4,从而可得cn=bn2-anbn=4n+16,易求cn+1-cn=4,从而可得答案.
解答:
解:∵f(x)=(x-1)2+n,x∈[-1,3],
∴当x=1时,f(x)min=an=n,
当x=-1或x=3时,f(x)max=bn=n+4;
∴cn=bn2-anbn=(n+4)2-n(n+4)=4n+16,
∵cn+1-cn=4,
∴数列{cn}是公差不为0的等差数列,
故选:C.
∴当x=1时,f(x)min=an=n,
当x=-1或x=3时,f(x)max=bn=n+4;
∴cn=bn2-anbn=(n+4)2-n(n+4)=4n+16,
∵cn+1-cn=4,
∴数列{cn}是公差不为0的等差数列,
故选:C.
点评:本题考查等差关系的确定,求得an=n,bn=n+4是关键,考查等价转化思想与运算求解能力,属于中档题.

练习册系列答案
相关题目
在△ABC中,若tanAtanB=1,则△ABC的形状是( )
| A、等边三角形 |
| B、等腰三角形 |
| C、等腰直角三角形 |
| D、直角三角形 |
已知函数f(x)=ax2+ax+4(0<a<2),若 x1<x2,x1+x2=1-a,则( )
| A、f(x1)>f(x2) |
| B、f(x1)<f(x2) |
| C、f(x1)=f(x2) |
| D、f(x1)与f(x2)的大小不能确定 |
“m=1”是“函数f(x)=x2-6mx+6在区间(-∞,3]上为减函数”的( )
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
设奇函数f(x)在(0,+∞)上为单调递增函数,且f(2)=0,则不等式f(x)≥0的解集为( )
| A、[-2,0]∪[2,+∞) |
| B、(-∞,-2]∪(0,2] |
| C、(-∞,-2]∪[2,+∞) |
| D、[-2,0)∪(0,2] |
函数y=2sinx,x∈[
,
]和y=2的图象围成了一个封闭图形,则此封闭图形的面积是( )
| π |
| 2 |
| 5π |
| 2 |
| A、4 | B、2π | C、4π | D、8π |
已知点P(x,y)的坐标满足
,则(x-1)2+y2的取值范围是( )
|
A、[
| ||
B、[
| ||
| C、[1,9) | ||
D、[
|
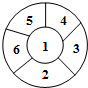 如图,有一个圆环型花圃,要在花圃的6个部分栽种4种不同颜色的花,每部分栽种1种,且相邻部分栽种不同颜色的花,则不同的栽种方法有
如图,有一个圆环型花圃,要在花圃的6个部分栽种4种不同颜色的花,每部分栽种1种,且相邻部分栽种不同颜色的花,则不同的栽种方法有