题目内容
将4个不同颜色的小球全部放入不同标号的3个盒子中,可以有一个或者多个盒子空着的放法种数为( )
| A、96 | B、36 | C、64 | D、81 |
考点:排列、组合及简单计数问题
专题:应用题,排列组合
分析:根据题意,每个小球有3种方法,由分步计数原理计算可得答案.
解答:
解:根据题意,每个小球有3种方法,共有3×3×3×3=34=81种放法,
故选D.
故选D.
点评:本题考查分步计数原理的运用,灵活运用分步计数原理是本题的关键.

练习册系列答案
相关题目
已知函数y=f(x)和y=g(x)的图象如图,则有( )
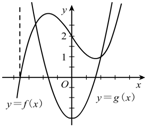

| A、f′(x)=g(x) |
| B、g′(x)=f(x) |
| C、f′(x)=g′(x) |
| D、g(x)=f(x) |
“m=1”是“函数f(x)=x2-6mx+6在区间(-∞,3]上为减函数”的( )
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
若集合A={x|x≥0},且A∩B=B,则集合B可能是( )
| A、{1,2} |
| B、{x|x≤1} |
| C、{-1,0,1} |
| D、R |
如图,在正方形ABCD中,E为AB中点,BF⊥CE于F,那么S△BFC:S正方形ABCD=( )
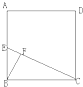

| A、1:3 | B、1:4 |
| C、1:5 | D、1:6 |
已知直线l:x+my+4=0,若曲线x2+y2+2x-6y+1=0上存在两点P、Q关于直线l对称,则m的值为( )
| A、2 | B、-2 | C、1 | D、-1 |
函数y=
的定义域是( )
| ||
| tanx |
A、{x|2kπ≤x≤2kπ+
| ||||
B、{x|2kπ<x<2kπ+
| ||||
| C、{x|2kπ<x<2kπ+π,k∈Z} | ||||
D、{x|2kπ-
|