题目内容
将函数f（x）=2sin（2x-θ）-3的图象F，向左平移
个单位，向上平移3个单位得到图象F′，若F′的一条对称轴是直线x=
，则θ的一个可能取值是（ ）
| π |
| 6 |
| π |
| 4 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：由条件根据函数y=Asin（ωx+φ）的图象变换规律，可得F′对应的函数的解析式为y=2sin（2x+
-θ）．再根据F′的一条对称轴是直线x=
，求得θ的一个可能取值．
| π |
| 3 |
| π |
| 4 |
解答：
解：将函数f（x）=2sin（2x-θ）-3的图象F，向左平移
个单位，可得函数y=2sin[2（x+
）-θ]-3=2sin（2x+
-θ）-3的图象；
再把所得图象向上平移3个单位得到图象F′，故F′对应的函数的解析式为y=2sin（2x+
-θ）．
若F′的一条对称轴是直线x=
，则有 2×
+
-θ=kπ+
，k∈z，即θ=
-kπ，则θ的一个可能取值是
，
故选：D．
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
再把所得图象向上平移3个单位得到图象F′，故F′对应的函数的解析式为y=2sin（2x+
| π |
| 3 |
若F′的一条对称轴是直线x=
| π |
| 4 |
| π |
| 4 |
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
故选：D．
点评：本题主要考查函数y=Asin（ωx+φ）的图象变换规律，正弦函数的图象的对称性，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f（x）=sin x+ln x，则f′（1）的值为（ ）
| A、1-cos 1 |
| B、1+cos 1 |
| C、cos 1-1 |
| D、-1-cos 1 |
在△ABC中，若tanAtanB=1，则△ABC的形状是（ ）
| A、等边三角形 |
| B、等腰三角形 |
| C、等腰直角三角形 |
| D、直角三角形 |
已知函数y=f（x）和y=g（x）的图象如图，则有（ ）
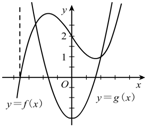
| A、f′（x）=g（x） |
| B、g′（x）=f（x） |
| C、f′（x）=g′（x） |
| D、g（x）=f（x） |
“m=1”是“函数f（x）=x2-6mx+6在区间（-∞，3]上为减函数”的（ ）
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
如图，在正方形ABCD中，E为AB中点，BF⊥CE于F，那么S△BFC：S正方形ABCD=（ ）
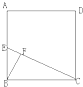
| A、1：3 | B、1：4 |
| C、1：5 | D、1：6 |
与-525°的终边相同的角可表示为（ ）
| A、525°-k•360°（k∈Z） |
| B、165°+k•360°（k∈Z） |
| C、195°+k•360°（k∈Z） |
| D、-195°+k•360°（k∈Z） |