题目内容
给出下列命题:
①若函数f(x)=asinx+cosx的一个对称中心是(
,0),则a的值为-
;
②函数f(x)=cos(2x+
)在区间[0,
]上单调递减;
③已知函数f(x)=sin(2x+ϕ)(-π<ϕ<π),若-|f(
)|≤f(x)对任意x∈R恒成立,则ϕ=
或-
;
④函数f(x)=|sin(2x-
)+1|的最小正周期为π.
其中正确结论的序号是 .
①若函数f(x)=asinx+cosx的一个对称中心是(
| π |
| 6 |
| 3 |
②函数f(x)=cos(2x+
| π |
| 2 |
| π |
| 2 |
③已知函数f(x)=sin(2x+ϕ)(-π<ϕ<π),若-|f(
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
④函数f(x)=|sin(2x-
| π |
| 3 |
其中正确结论的序号是
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:将(
,0)代入可判断①;根据余弦函数的单调性,可判断②;根据正弦函数的最值,可判断③,根据正弦型函数的周期性,可判断④
| π |
| 6 |
解答:
解:将(
,0)代入f(x)=asinx+cosx得:
a+
=0,解得a=-
,故①正确;
由2x+
∈[2kπ,2kπ+π],k∈Z得:x∈[kπ-
,kπ+
],k∈Z,故函数f(x)=cos(2x+
)在区间[0,
]上单调递减,在[
,
]上递增,故②错误;
由已知可得f(
)为函数f(x)的最值,故2×
+ϕ=
+2kπ,k∈Z,又由-π<ϕ<π可得:ϕ=
或-
,故③正确;
函数y=sin(2x-
)+1的最小正周期为π,函数f(x)=|sin(2x-
)+1|=sin(2x-
)+1,故④正确;
故答案为:①③④
| π |
| 6 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
由2x+
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
由已知可得f(
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| 5π |
| 6 |
函数y=sin(2x-
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
故答案为:①③④
点评:本题考查的知识点是函数y=Asin(ωx+φ)的图象和性质,熟练掌握函数y=Asin(ωx+φ)的图象和性质是解答的关键,难度中档.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
已知函数f(x)=sin x+ln x,则f′(1)的值为( )
| A、1-cos 1 |
| B、1+cos 1 |
| C、cos 1-1 |
| D、-1-cos 1 |
“m=1”是“函数f(x)=x2-6mx+6在区间(-∞,3]上为减函数”的( )
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
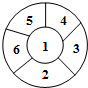 如图,有一个圆环型花圃,要在花圃的6个部分栽种4种不同颜色的花,每部分栽种1种,且相邻部分栽种不同颜色的花,则不同的栽种方法有
如图,有一个圆环型花圃,要在花圃的6个部分栽种4种不同颜色的花,每部分栽种1种,且相邻部分栽种不同颜色的花,则不同的栽种方法有