题目内容
某代表团在某次人代会上准备提交有关教育、医疗、环保、民生四个方面的议案共11条,提交之间要先在小组内进行逐条讨论(任意一条被等可能的讨论).假设在前两条被讨论的议案中至少有1条是教育类的概率是
.
(Ⅰ)求教育类的议案的条数;
(Ⅱ)在先被讨论的4条议案中,记教育类的条数为X,求X的分布列与数学期望E(X).
| 34 |
| 55 |
(Ⅰ)求教育类的议案的条数;
(Ⅱ)在先被讨论的4条议案中,记教育类的条数为X,求X的分布列与数学期望E(X).
考点:离散型随机变量的期望与方差,等可能事件的概率
专题:概率与统计
分析:(I)设教育类的议案有x条,则1-
=
,解得即可.
(II)由题设知,X=0,1,2,3,4先分别求出P(X),由此能求出X的分布列和期望.
| ||
|
| 34 |
| 35 |
(II)由题设知,X=0,1,2,3,4先分别求出P(X),由此能求出X的分布列和期望.
解答:
解:(Ⅰ)设教育类的议案有x条,则1-
=
,∴x=4,教育类的议案有4条;
(Ⅱ)X的可能取值为0,1,2,3,4,
P(X=0)=
=
,P(X=1)=
=
,P(X=2)=
=
,P(X=3)=
=
,P(X=4)=
,
∴X的分布列为
∴E(X)=0×
+1×
+2×
+3×
+4×
=
| ||
|
| 34 |
| 35 |
(Ⅱ)X的可能取值为0,1,2,3,4,
P(X=0)=
| ||
|
| 7 |
| 66 |
| ||||
|
| 14 |
| 33 |
| ||||
|
| 21 |
| 55 |
| ||||
|
| 14 |
| 165 |
| ||
|
∴X的分布列为
| X | 0 | 1 | 2 | 3 | 4 | ||||||||||
| P |
|
|
|
|
|
| 7 |
| 66 |
| 14 |
| 33 |
| 21 |
| 55 |
| 14 |
| 165 |
| 1 |
| 330 |
| 16 |
| 11 |
点评:本题考查离散型随机变量的分布列、数学期望,是中档题.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
有一段演绎推理是这样的:“若直线平行于平面,则该直线平行于平面内所有直线:已知直线b∥平面α,直线a?平面α,则直线b∥直线a”,结论显然是错误的,这是因为( )
| A、大前提错误 |
| B、小前提错误 |
| C、推理形式错误 |
| D、非以上错误 |
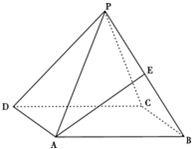 正四棱锥P-ABCD中,侧面与底面ABCD所成的角为60°,E是PB的中点,求异面直线PD与AE所成角的大小.
正四棱锥P-ABCD中,侧面与底面ABCD所成的角为60°,E是PB的中点,求异面直线PD与AE所成角的大小.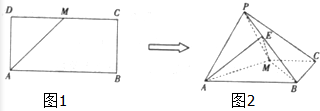 如图,已知长方形ABCD中,AB=2,AD=1,M为DC的中点.将△ADM沿AM折起到△APM,使得平面APM⊥平面ABCM,点E在线段PB上,且PE=
如图,已知长方形ABCD中,AB=2,AD=1,M为DC的中点.将△ADM沿AM折起到△APM,使得平面APM⊥平面ABCM,点E在线段PB上,且PE=