题目内容
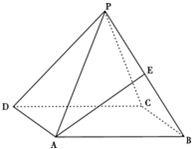 正四棱锥P-ABCD中,侧面与底面ABCD所成的角为60°,E是PB的中点,求异面直线PD与AE所成角的大小.
正四棱锥P-ABCD中,侧面与底面ABCD所成的角为60°,E是PB的中点,求异面直线PD与AE所成角的大小.考点:异面直线及其所成的角
专题:空间角
分析:解:连接AC、BD交于点O,连接PO,连接EO,由已知条件推导出∠AEO就是异面直线PD与AE所成的角,由此能求出异面直线PD与AE所成角的大小.
解答:
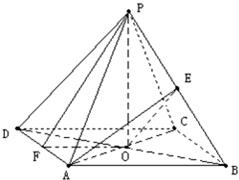 解:连接AC、BD交于点O,连接PO,则PO⊥面ABCD,
解:连接AC、BD交于点O,连接PO,则PO⊥面ABCD,
设F为AD中点,连FO、PF,
由题意知OF⊥AD,PF⊥AD,
∴∠PFO就是侧面PAD与底面ABCD所成二面角的平面角.
∴∠PFO=60°,
即侧面PAD与底面ABCD所成二面角的大小为60°
连接EO,由于O为BD中点,E为PB中点,
∴EO∥PD,EO=
PD,
∴∠AEO就是异面直线PD与AE所成的角,
不妨设底面正方形边长为1,DO=AO=
,PO=1
在Rt△POD中,PD=
=
,∴EO=
,
由AO⊥BD,AO⊥PO可知AO⊥面PBD.∴AO⊥EO
在Rt△AOE中,tan∠AEO=
=
,
∴异面直线PD与AE所成角为arctan
.
 解:连接AC、BD交于点O,连接PO,则PO⊥面ABCD,
解:连接AC、BD交于点O,连接PO,则PO⊥面ABCD,设F为AD中点,连FO、PF,
由题意知OF⊥AD,PF⊥AD,
∴∠PFO就是侧面PAD与底面ABCD所成二面角的平面角.
∴∠PFO=60°,
即侧面PAD与底面ABCD所成二面角的大小为60°
连接EO,由于O为BD中点,E为PB中点,
∴EO∥PD,EO=
| 1 |
| 2 |
∴∠AEO就是异面直线PD与AE所成的角,
不妨设底面正方形边长为1,DO=AO=
| ||
| 2 |
在Rt△POD中,PD=
| OD2+PO2 |
| ||
| 2 |
| ||
| 4 |
由AO⊥BD,AO⊥PO可知AO⊥面PBD.∴AO⊥EO
在Rt△AOE中,tan∠AEO=
| AO |
| EO |
2
| ||
| 5 |
∴异面直线PD与AE所成角为arctan
2
| ||
| 5 |
点评:本题考查直线与平面所成角的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
在正态分布N(0,
)中,数值落在(-∞,-1)∪(1,+∞)内的概率为( )
| 1 |
| 9 |
| A、0.097 |
| B、0.046 |
| C、0.03 |
| D、0.0026 |
若关于x的一元二次不等式ax2+bx+c>0的解集是空集,则( )
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
某大学有本科生8000人,其中一、二、三、四年级的学生比为5:4:3:1,要用分层抽样的方法从所有本科生中抽取一个容量为260的样本,则应抽二年级的学生( )
| A、100人 | B、60人 |
| C、80人 | D、20人 |