题目内容
若直线l:y=kx+
与双曲线
-y2=1恒有两个不同的交点A和B,且
•
>2(其中O为原点),求k的取值范围.
| 2 |
| x2 |
| 3 |
| OA |
| OB |
考点:直线与圆锥曲线的关系
专题:圆锥曲线中的最值与范围问题
分析:联立直线和双曲线方程,转化为一元二次方程,利用根与系数之间的关系即可求出k的取值范围.
解答:
解:由将y=kx+
代入双曲线
-y2=1消去y得(1-3k2)x2-6
kx-9=0.
由直线l与双曲线交于不同的两点得
即k2≠
且k2<1.①
设A(xA,yA),B(xB,yB),则 xA+xB=
,xAxB=
.
由
•
>2,得xAxB+yAyB>2,
即xAxB+yAyB=xAxB+(kxA+
)(kxB+
)=(k2+1)xAxB+
k(xA+xB)+2=)=(k2+1)•
+
k(
)+2=
.
于是
>2,即
>0,
解此不等式得
<k2<3.②
由①②得
<k2<1.
故k的取值范围为(-1,-
)∪(
,1).
| 2 |
| x2 |
| 3 |
| 2 |
由直线l与双曲线交于不同的两点得
|
即k2≠
| 1 |
| 3 |
设A(xA,yA),B(xB,yB),则 xA+xB=
6
| ||
| 1-3k2 |
| -9 |
| 1-3k2 |
由
| OA |
| OB |
即xAxB+yAyB=xAxB+(kxA+
| 2 |
| 2 |
| 2 |
| -9 |
| 1-3k2 |
| 2 |
6
| ||
| 1-3k2 |
| 3k2+7 |
| 3k2-1 |
于是
| 3k2+7 |
| 3k2-1 |
| -3k2+9 |
| 3k2-1 |
解此不等式得
| 1 |
| 3 |
由①②得
| 1 |
| 3 |
故k的取值范围为(-1,-
| ||
| 3 |
| ||
| 3 |
点评:本题主要考查直线和双曲线的位置关系,利用直线和双曲线联立转化为一元二次方程,利用根与系数之间的关系是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
直线l的方向向量与平面α的法向量的夹角为150°,则l与平面α所成的角为( )
| A、120° | B、30° |
| C、60° | D、150° |
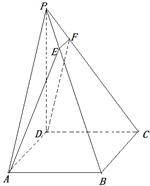 如图,已知ABCD是正方形,PD⊥平面ABCD,
如图,已知ABCD是正方形,PD⊥平面ABCD,