题目内容
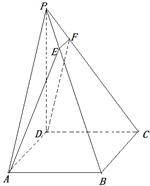 如图,已知ABCD是正方形,PD⊥平面ABCD,PD=
如图,已知ABCD是正方形,PD⊥平面ABCD,PD=| 3 |
(1)求证:BC∥EF;
(2)求二面角A-PB-D的余弦值.
考点:二面角的平面角及求法,直线与平面平行的性质
专题:空间位置关系与距离,空间角
分析:(1)根据线面平行的性质定理,证明BC∥平面AEFD,即可证明BC∥EF;
(2)根据二面角平面角的定义,确定平面角,然后根据三角形的边角关系,即可求二面角A-PB-D的余弦值.
(2)根据二面角平面角的定义,确定平面角,然后根据三角形的边角关系,即可求二面角A-PB-D的余弦值.
解答:
证明:(1)∵BC∥AD,
∴BC∥平面AEFD.
又∵BC?平面BCP,EF为平面ADE与平面BCP的交线,
∴BC∥EF.
(2)连结AC交BD于O,则AO⊥BD,AO⊥PD.
∴AO⊥平面PDB.作AM⊥PB于M,连结OM.
则∠AMO为二面角APBD的平面角.
设AD=1,则PD=
,PA=2.
AM=
=
=
,AO=
.
∴sin∠AMO=
=
.
cos∠AMO=
=
.
∴BC∥平面AEFD.
又∵BC?平面BCP,EF为平面ADE与平面BCP的交线,
∴BC∥EF.
(2)连结AC交BD于O,则AO⊥BD,AO⊥PD.
∴AO⊥平面PDB.作AM⊥PB于M,连结OM.
则∠AMO为二面角APBD的平面角.
设AD=1,则PD=
| 3 |

AM=
| PA•AB |
| PB |
| 2 | ||
|
2
| ||
| 5 |
| ||
| 2 |
∴sin∠AMO=
| A0 |
| AM |
| ||
| 4 |
cos∠AMO=
1-(
|
| ||
| 4 |
点评:本题主要考查空间直线平行的判断,以及空间二面角的大小求法,考查学生的运算能力.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
把函数y=cosx的图象向左平移
个单位,然后把,图象上的所有点的横坐标缩小到原来的
(纵坐标不变),则所得图形对应的函数解析式为( )
| π |
| 4 |
| 1 |
| 2 |
A、y=cos(
| ||||
B、y=cos(2x+
| ||||
C、y=cos(
| ||||
D、y=cos(2x+
|
如图所示是《函数的应用》的知识结构图,如果要加入“用二分法求方程的近似解”,则应该放在( )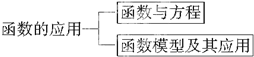

| A、“函数与方程”的上位 |
| B、“函数与方程”的下位 |
| C、“函数模型及其应用”的上位 |
| D、“函数模型及其应用”的下位 |
 如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=4,AD=2,PA=2,PD=
如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=4,AD=2,PA=2,PD= 如图,在三棱锥P-ABC中,PA=PB=AB=BC,∠PBC=90°,D为AC的中点,AB⊥PD.
如图,在三棱锥P-ABC中,PA=PB=AB=BC,∠PBC=90°,D为AC的中点,AB⊥PD.