题目内容
已知向量:
=(2cos(x-
),2sin(x-
)),
=(cos(x-
),sin(x+
)),(x∈R),函数f(x)=
•
-1.
(1)求函数f(x)的最小正周期和图象的对称轴方程;
(2)求函数f(x)在区间[-
,
]上的值域.
| a |
| π |
| 6 |
| π |
| 4 |
| b |
| π |
| 6 |
| π |
| 4 |
| a |
| b |
(1)求函数f(x)的最小正周期和图象的对称轴方程;
(2)求函数f(x)在区间[-
| π |
| 12 |
| π |
| 2 |
考点:两角和与差的正弦函数,三角函数的周期性及其求法,正弦函数的对称性
专题:三角函数的求值
分析:(1)由数量积和三角函数的运算化简可得f(x)=sin(2x-
),易得周期和对称轴方程;(2)由x∈[-
,
]可得2x-
∈[-
,
],由三角函数的单调性可得值域.
| π |
| 6 |
| π |
| 12 |
| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
| 5π |
| 6 |
解答:
解:(1)∵
=(2cos(x-
),2sin(x-
)),
=(cos(x-
),sin(x+
)),
∴f(x)=
•
-1=2cos2(x-
)+2sin(x-
)sin(x+
)-1
=2cos2(x-
)-1-2sin(
-x)cos(
-x)
=cos(2x-
)-sin(
-2x)
=
cos2x+
sin2x-cos2x
=
sin2x-
cos2x=sin(2x-
)
∴周期T=
=π
由2x-
=kπ+
(k∈Z),得x=
+
(k∈Z).
∴函数图象的对称轴方程为x=
+
(k∈Z)
(2)∵x∈[-
,
],∴2x-
∈[-
,
].
∵f(x)=sin(2x-
)在区间[-
,
]上单调递增,在区间[
,
]上单调递减,
∴当x=
时,f(x)取得最大值1,又∵f(-
)=-
<f(
)=
,
∴当x=-
时,f(x)取得最小值-
.
∴函数f(x)在[-
,
]上的值域为[-
,1]
| a |
| π |
| 6 |
| π |
| 4 |
| b |
| π |
| 6 |
| π |
| 4 |
∴f(x)=
| a |
| b |
| π |
| 6 |
| π |
| 4 |
| π |
| 4 |
=2cos2(x-
| π |
| 6 |
| π |
| 4 |
| π |
| 4 |
=cos(2x-
| π |
| 3 |
| π |
| 2 |
=
| 1 |
| 2 |
| ||
| 2 |
=
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
∴周期T=
| 2π |
| 2 |
由2x-
| π |
| 6 |
| π |
| 2 |
| kπ |
| 2 |
| π |
| 3 |
∴函数图象的对称轴方程为x=
| kπ |
| 2 |
| π |
| 3 |
(2)∵x∈[-
| π |
| 12 |
| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
| 5π |
| 6 |
∵f(x)=sin(2x-
| π |
| 6 |
| π |
| 12 |
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
∴当x=
| π |
| 3 |
| π |
| 12 |
| ||
| 2 |
| π |
| 2 |
| 1 |
| 2 |
∴当x=-
| π |
| 12 |
| ||
| 2 |
∴函数f(x)在[-
| π |
| 12 |
| π |
| 2 |
| ||
| 2 |
点评:本题考查两角和与差的正弦函数公式,涉及向量的运算和三角函数的值域,属中档题.

练习册系列答案
相关题目
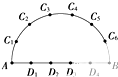 如图,在以AB为直径的半圆周上,有异于A、B的六个点C1、C2、C3、C4、C5、C6,直径AB上有异于A、B的四个点D1、D2、D3、D4.以这10个点中的3个点为顶点作三角形可作出多少个( )
如图,在以AB为直径的半圆周上,有异于A、B的六个点C1、C2、C3、C4、C5、C6,直径AB上有异于A、B的四个点D1、D2、D3、D4.以这10个点中的3个点为顶点作三角形可作出多少个( ) 如图,在三棱锥P-ABC中,PA=PB=AB=BC,∠PBC=90°,D为AC的中点,AB⊥PD.
如图,在三棱锥P-ABC中,PA=PB=AB=BC,∠PBC=90°,D为AC的中点,AB⊥PD.