题目内容
如图，已知三棱锥O-ABC的侧棱OA，OB，OC两两垂直，且OA=1，OB=OC=2，E是OC的中点．
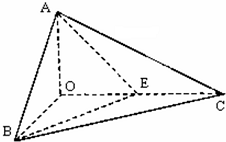
（1）求异面直线EB与AC所成角的余弦值；
（2）求点E到面ABC的距离．
（3）求二面角E-AB-C的平面角的正切值．
（1）求异面直线EB与AC所成角的余弦值；
（2）求点E到面ABC的距离．
（3）求二面角E-AB-C的平面角的正切值．
考点：用空间向量求平面间的夹角,异面直线及其所成的角,二面角的平面角及求法
专题：计算题,空间位置关系与距离,空间角
分析：（1）以O为原点，OB、OC、OA分别为x、y、z轴建立空间直角坐标系，求出
=（2，-1，0），
=（0，2，-1）
可得cos＜
，
＞=
=-
；
（2）求出平面ABC的法向量
=（1，1，2），即可点E到面ABC的距离d=
；
（3）求出平面EAB的法向量，利用向量的夹角公式，即可得出结论．
| EB |
| AC |
可得cos＜
| EB |
| AC |
| -2 | ||||
|
| 2 |
| 5 |
（2）求出平面ABC的法向量
| n |
|
| ||||
|
|
（3）求出平面EAB的法向量，利用向量的夹角公式，即可得出结论．
解答：
解：（1）以O为原点，OB、OC、OA分别为x、y、z轴建立空间直角坐标系．
则有A（0，0，1）、B（2，0，0）、C（0，2，0）、E（0，1，0）
∴
=（2，-1，0），
=（0，2，-1）
∴cos＜
，
＞=
=-
，
∴异面直线BE与AC所成角的余弦为
；
（2）设平面ABC的法向量为
=（x，y，z），则
∵
=（2，0，-1），
=（0，2，-1），
∴
，
∴取
=（1，1，2）
又
=（0，1，0），
∴点E到面ABC的距离d=
=
；
（3）（2）中已求平面ABC的法向量
=（1，1，2），
设平面EAB的法向量为
=（a，b，c），则
∵
=（0，1，-1），
=（2，0，-1），
∴
∴取
=（1，2，2），
∴cos＜
，
＞=
设二面角E-AB-C的平面角为θ，则tanθ=
．
解：（1）以O为原点，OB、OC、OA分别为x、y、z轴建立空间直角坐标系．则有A（0，0，1）、B（2，0，0）、C（0，2，0）、E（0，1，0）
∴
| EB |
| AC |
∴cos＜
| EB |
| AC |
| -2 | ||||
|
| 2 |
| 5 |
∴异面直线BE与AC所成角的余弦为
| 2 |
| 5 |
（2）设平面ABC的法向量为
| n |
∵
| AB |
| AC |
∴
|
∴取
| n |
又
| EC |
∴点E到面ABC的距离d=
|
| ||||
|
|
| ||
| 6 |
（3）（2）中已求平面ABC的法向量
| n |
设平面EAB的法向量为
| m |
∵
| AE |
| AB |
∴
|
∴取
| m |
∴cos＜
| n |
| m |
7
| ||
| 18 |
设二面角E-AB-C的平面角为θ，则tanθ=
| ||
| 7 |
点评：本题主要考察了空间中异面直线所成的角和平面与平面所成的角，属立体几何中的常考题型，较难．解题的关键是首先正确的建立空间直角坐标系然后可将异面直线所成的角转化为所对应的向量的夹角或其补角．
练习册系列答案
相关题目
三次函数f（x）=ax3+2x+5在x∈（-∞，+∞）内是增函数，则（ ）
| A、a＞0 | ||
| B、a＜0 | ||
| C、a=1 | ||
D、a=
|
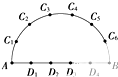如图，在以AB为直径的半圆周上，有异于A、B的六个点C1、C2、C3、C4、C5、C6，直径AB上有异于A、B的四个点D1、D2、D3、D4．以这10个点中的3个点为顶点作三角形可作出多少个（ ）| A、116 | B、128 |
| C、215 | D、98 |
现有数列{an}满足：a1=1，且对任意的m，n∈N*都有：am+n=am+an+mn，则
+
+
+…+
=
（ ）
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a2014 |
（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
如图所示是《函数的应用》的知识结构图，如果要加入“用二分法求方程的近似解”，则应该放在（ ）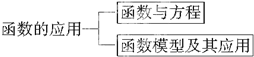
| A、“函数与方程”的上位 |
| B、“函数与方程”的下位 |
| C、“函数模型及其应用”的上位 |
| D、“函数模型及其应用”的下位 |
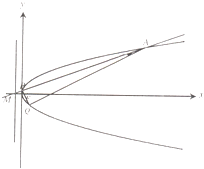在平面直角坐标系xOy中，已知抛物线C：y2=2px（p＞0），在此抛物线上一点M（2，m）到焦点的距离是3．