题目内容
直线l的方向向量与平面α的法向量的夹角为150°，则l与平面α所成的角为（ ）
| A、120° | B、30° |
| C、60° | D、150° |
考点：直线与平面所成的角
专题：空间角
分析：由已知条件知直线l的方向向量与平面α的法向量小的夹角等于30°，由此能求出直线l与平面α所成的角的大小．
解答：
解：∵直线l的方向向量与平面α的法向量大的夹角等于150°，
∴直线l的方向向量与平面α的法向量小的夹角等于30°
∴直线l与平面α所成的角等于60°．
故选：C．
∴直线l的方向向量与平面α的法向量小的夹角等于30°
∴直线l与平面α所成的角等于60°．
故选：C．
点评：本题考查直线与平面所成的角的大小的求法，是基础题，解题时要认真审题，注意法向量和方向向量知识的合理运用．
练习册系列答案
孟建平名校考卷系列答案
相关题目
已知函数f（x）的导函数为f′（x），且满足f（x）=2xf′（
）+cosx，则f′（
）的值为（ ）
| π |
| 2 |
| π |
| 4 |
A、2+
| ||||
B、2-
| ||||
C、
| ||||
D、-
|
三次函数f（x）=ax3+2x+5在x∈（-∞，+∞）内是增函数，则（ ）
| A、a＞0 | ||
| B、a＜0 | ||
| C、a=1 | ||
D、a=
|
已知a是2和6的等差中项，则a为（ ）
A、2
| ||
B、
| ||
| C、4 | ||
| D、3 |
把函数y=cosx的图象向左平移
个单位，然后把，图象上的所有点的横坐标缩小到原来的
（纵坐标不变），则所得图形对应的函数解析式为（ ）
| π |
| 4 |
| 1 |
| 2 |
A、y=cos（
| ||||
B、y=cos（2x+
| ||||
C、y=cos（
| ||||
D、y=cos（2x+
|
复数
等于（ ）
| 1-2i |
| 3+i |
A、
| ||
B、
| ||
C、
| ||
D、
|
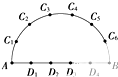如图，在以AB为直径的半圆周上，有异于A、B的六个点C1、C2、C3、C4、C5、C6，直径AB上有异于A、B的四个点D1、D2、D3、D4．以这10个点中的3个点为顶点作三角形可作出多少个（ ）| A、116 | B、128 |
| C、215 | D、98 |
现有数列{an}满足：a1=1，且对任意的m，n∈N*都有：am+n=am+an+mn，则
+
+
+…+
=
（ ）
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a2014 |
（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|