题目内容
9.已知集合A={1,a2},B={1,2,a},若A⊆B,求实数a的值.分析 由{1,a2}⊆{1,2,a},从而讨论a2=2或a2=a,注意元素的互异性即可.
解答 解:∵{1,a2}⊆{1,2,a},
∴①若a2=2,则a=$\sqrt{2}$或-$\sqrt{2}$;
经检验成立;
②若a2=a,则a=0或1;
经检验,a=1不成立;
综上所述,a=±$\sqrt{2}$或0.
点评 本题考查了集合的包含关系的应用及分类讨论的应用.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
19.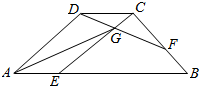 如图,在梯形ABCD中,AB=3CD=4AE,BC=3BF,DF交EC于点G,若$\overrightarrow{AG}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$,则$\frac{m}{n}$等于( )
如图,在梯形ABCD中,AB=3CD=4AE,BC=3BF,DF交EC于点G,若$\overrightarrow{AG}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$,则$\frac{m}{n}$等于( )
 如图,在梯形ABCD中,AB=3CD=4AE,BC=3BF,DF交EC于点G,若$\overrightarrow{AG}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$,则$\frac{m}{n}$等于( )
如图,在梯形ABCD中,AB=3CD=4AE,BC=3BF,DF交EC于点G,若$\overrightarrow{AG}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$,则$\frac{m}{n}$等于( )| A. | $\frac{11}{6}$ | B. | $\frac{3}{2}$ | C. | $\frac{14}{33}$ | D. | $\frac{35}{56}$ |
4.圆O:x2+y2-2x-7=0与直线l:(λ+1)x-y+1-λ=0(λ∈R)的位置关系是( )
| A. | 相切 | B. | 相交 | C. | 相离 | D. | 不确定 |
14.若直线x+y-a=0被圆x2+y2=4截得的弦长为2$\sqrt{2}$,则实数a的值为( )
| A. | 2$\sqrt{7}$或-2$\sqrt{7}$ | B. | 2或-2 | C. | 2 | D. | -2 |
1.下列说法中:
①平行于同一直线的两个平面平行;
②平行于同一平面的两个不同平面平行;
③垂直于同一直线的两条直线平行;
④垂直于同一平面的两条不重合直线平行;
其中正确的说法个数为( )
①平行于同一直线的两个平面平行;
②平行于同一平面的两个不同平面平行;
③垂直于同一直线的两条直线平行;
④垂直于同一平面的两条不重合直线平行;
其中正确的说法个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
17.过抛物线y2=2px(p>0)的焦点F且倾斜角为α的直线交抛物线于A、B两点,若S△ADF=4S△BOF,O为坐标原点,则sinα=( )
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |