题目内容
14.若直线x+y-a=0被圆x2+y2=4截得的弦长为2$\sqrt{2}$,则实数a的值为( )| A. | 2$\sqrt{7}$或-2$\sqrt{7}$ | B. | 2或-2 | C. | 2 | D. | -2 |
分析 利用直线x+y-a=0被圆x2+y2=4截得的弦长为2$\sqrt{2}$,可得圆心到直线的距离d=$\frac{|a|}{\sqrt{2}}$=$\sqrt{4-2}$,即可求出实数a的值.
解答 解:∵直线x+y-a=0被圆x2+y2=4截得的弦长为2$\sqrt{2}$,
∴圆心到直线的距离d=$\frac{|a|}{\sqrt{2}}$=$\sqrt{4-2}$,
∴a=±2,
故选:B.
点评 本题考查直线与圆的位置关系,考查点到直线的距离公式,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
5.设ABCD-A1B1C1D1是棱长为的a的正方体,则有( )
| A. | $\overrightarrow{AB}•\overrightarrow{{C_1}A}={a^2}$ | B. | $\overrightarrow{AB}•\overrightarrow{{A_1}{C_1}}=\sqrt{2}{a^2}$ | C. | $\overrightarrow{BC}•\overrightarrow{{A_1}D}={a^2}$ | D. | $\overrightarrow{AB}•\overrightarrow{{C_1}{A_1}}={a^2}$ |
3.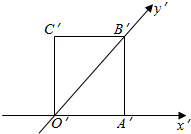 如图的正方形O′A′B′C′的边长为1cm,它是水平放置的一个平面图形的直观图,则原图形的面积为( )
如图的正方形O′A′B′C′的边长为1cm,它是水平放置的一个平面图形的直观图,则原图形的面积为( )
 如图的正方形O′A′B′C′的边长为1cm,它是水平放置的一个平面图形的直观图,则原图形的面积为( )
如图的正方形O′A′B′C′的边长为1cm,它是水平放置的一个平面图形的直观图,则原图形的面积为( )| A. | 2$\sqrt{2}$cm2 | B. | 1cm2 | C. | 4$\sqrt{2}$cm2 | D. | $\frac{\sqrt{2}}{4}$cm2 |