题目内容
19.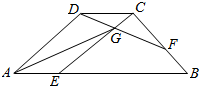 如图,在梯形ABCD中,AB=3CD=4AE,BC=3BF,DF交EC于点G,若$\overrightarrow{AG}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$,则$\frac{m}{n}$等于( )
如图,在梯形ABCD中,AB=3CD=4AE,BC=3BF,DF交EC于点G,若$\overrightarrow{AG}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$,则$\frac{m}{n}$等于( )| A. | $\frac{11}{6}$ | B. | $\frac{3}{2}$ | C. | $\frac{14}{33}$ | D. | $\frac{35}{56}$ |
分析 用$\overrightarrow{AB},\overrightarrow{AD}$表示出$\overrightarrow{AG}$,根据平面向量的基本定理求出m,n.
解答 解:$\overrightarrow{BC}$=$\overrightarrow{AC}-\overrightarrow{AB}$=$\overrightarrow{AD}+\overrightarrow{DC}-\overrightarrow{AB}$=$\overrightarrow{AD}-\frac{2}{3}\overrightarrow{AB}$,
$\overrightarrow{EC}=\overrightarrow{EB}+\overrightarrow{BC}$=$\frac{3}{4}$$\overrightarrow{AB}$+$\overrightarrow{BC}$=$\frac{1}{12}\overrightarrow{AB}$+$\overrightarrow{AD}$,$\overrightarrow{FD}=\overrightarrow{FC}+\overrightarrow{CD}$=$\frac{2}{3}$$\overrightarrow{BC}-\frac{1}{3}\overrightarrow{AB}$=-$\frac{7}{9}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$,
设$\overrightarrow{EG}=λ\overrightarrow{EC}$,$\overrightarrow{DG}=μ\overrightarrow{FD}$,
则$\overrightarrow{AG}=\overrightarrow{AE}+\overrightarrow{EG}$=$\frac{1}{4}$$\overrightarrow{AB}$+$\frac{λ}{12}$$\overrightarrow{AB}$+$λ\overrightarrow{AD}$=($\frac{1}{4}+\frac{λ}{12}$)$\overline{AB}$+λ$\overrightarrow{AD}$,$\overrightarrow{AG}=\overrightarrow{AD}+\overrightarrow{DG}$=$\overrightarrow{AD}$+$\frac{2μ}{3}$$\overrightarrow{AD}$-$\frac{7}{9}$μ$\overrightarrow{AB}$=-$\frac{7}{9}$μ$\overrightarrow{AB}$+(1+$\frac{2μ}{3}$)$\overrightarrow{AD}$.
∴$\left\{\begin{array}{l}{\frac{1}{4}+\frac{λ}{12}=-\frac{7}{9}μ}\\{λ=1+\frac{2μ}{3}}\end{array}\right.$,解得$\left\{\begin{array}{l}{λ=\frac{11}{15}}\\{μ=-\frac{2}{5}}\end{array}\right.$,∴m=$\frac{14}{45}$,n=$\frac{11}{15}$.∴$\frac{m}{n}$=$\frac{14}{33}$.
故选:C.
点评 本题考查了平面向量的基本定理及向量加减运算的几何意义,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{6}$ |
| A. | e1e2=1 | B. | e1e2=2 | C. | e1+e2=2 | D. | $\frac{1}{{e}_{1}}$+$\frac{1}{{e}_{2}}$=2 |