题目内容
18.若点O和点F分别为椭圆3x2+4y2=12的中心和左焦点,点P为椭圆上任意一点,则$\overrightarrow{OP}•\overrightarrow{FP}$最大值为6.分析 设P(x,y),由数量积运算及点P在椭圆上可把$\overrightarrow{OP}•\overrightarrow{FP}$表示为x的二次函数,根据二次函数性质可求其最大值.
解答 解:设P(x,y),
则$\overrightarrow{OP}•\overrightarrow{FP}$=(x,y)•(x+1,y)=x2+x+y2,
又点P在椭圆上,故3x2+4y2=12,
所以x2+x+(3-$\frac{3}{4}$x2)=$\frac{1}{4}$x2+x+3=$\frac{1}{4}$(x+2)2+2,
又-2≤x≤2,
所以当x=2时,$\frac{1}{4}$(x+2)2+2取得最大值为6,即$\overrightarrow{OP}•\overrightarrow{FP}$的最大值为6,
故答案为:6.
点评 本题考查平面向量的数量积运算、椭圆的简单性质,属中档题.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
3.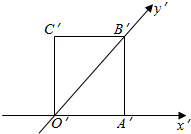 如图的正方形O′A′B′C′的边长为1cm,它是水平放置的一个平面图形的直观图,则原图形的面积为( )
如图的正方形O′A′B′C′的边长为1cm,它是水平放置的一个平面图形的直观图,则原图形的面积为( )
 如图的正方形O′A′B′C′的边长为1cm,它是水平放置的一个平面图形的直观图,则原图形的面积为( )
如图的正方形O′A′B′C′的边长为1cm,它是水平放置的一个平面图形的直观图,则原图形的面积为( )| A. | 2$\sqrt{2}$cm2 | B. | 1cm2 | C. | 4$\sqrt{2}$cm2 | D. | $\frac{\sqrt{2}}{4}$cm2 |
7.对于集合A、B,“A≠B”是“A∩B?A∪B”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |