题目内容
5．函数f（x）=sinx+x-1的图象在x=0处的切线方程为y=2x-1．分析 求出函数的导数，可得在x=0处切线的斜率，求得切点坐标，运用斜截式方程可得切线的方程．
解答 解：函数f（x）=sinx+x-1的导数为f′（x）=cosx+1，
图象在x=0处的切线斜率为cos0+1=2，
切点为（0，-1），
可得图象在x=0处的切线方程为y=2x-1．
故答案为：y=2x-1．
点评 本题考查导数的运用：求切线的方程，考查导数的几何意义，正确求导和运用直线方程是解题的关键，属于基础题．
练习册系列答案
相关题目
15．
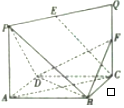如图，ACQP所在的平面与菱形ABCD所在的平面相互垂直，交线为AC，若$AC=\sqrt{2}AP，E，F$分别是PQ，CQ的中点．求证：
（1）CE∥平面PBD；
（2）平面FBD⊥平面PBD．
如图，ACQP所在的平面与菱形ABCD所在的平面相互垂直，交线为AC，若$AC=\sqrt{2}AP，E，F$分别是PQ，CQ的中点．求证：（1）CE∥平面PBD；
（2）平面FBD⊥平面PBD．
20．复数z满足$\overline{z}$（1-i）=|1+i|，则复数z的实部与虚部之和为（ ）
| A． | $\sqrt{2}$ | B． | -$\sqrt{2}$ | C． | 1 | D． | 0 |
17．执行如图的程序框图，若输入的a，b的值分别为0和9，则输出的i的值为（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |